Cardinality

Now we can define cardinality:

Cardinality

Let $A$ be a set. If $A$ is finite then $card (A) = | A |$ is just the number of elements in $A$ . Then:

$card (N) = ℵ_{0}$ (here $ℵ$ is called aleph, so this is aleph-null)
We know that since $R$ is uncountable then $card (R) = c$ where $c$ is the continuum.
$card (P (N)) > card (N)$ .
The set $A$ has the same cardinality as $B$ if $f : A \to B$ exists that is one-to-one and onto.
For same cardinality sets we write $A \sim B$ .

An example is as follows. The function $f (x) = \frac{x}{x^{2} - 1}$ takes the interval $(- 1, 1) \to R$ in a one-to-one correspondence, so $(- 1, 1) \sim R$ :

Proof
(injective) Instead suppose $f (x_{1}) = f (x_{2})$ . We'll show $x_{1} = x_{2}$ . Then:

\begin{aligned} \frac{x_{1}}{x_{1}^{2} - 1} & = \frac{x_{2}}{x_{2}^{2} - 1} \\ x_{1} (x_{2}^{2} - 1) & = x_{2} (x_{1}^{2} - 1) \\ x_{1} x_{2}^{2} + x_{2} - x_{2} x_{1}^{2} - x_{1} & = 0 & Solve for x_{2} \\ (x_{1}) x_{2}^{2} + (1 - x_{1}^{2}) x_{2} + (- x_{1}) 1 & = 0 \\ \frac{x_{1}^{2} - 1 \pm \sqrt{(1 - x_{1}^{2})^{2} + 4 x_{1}^{2}}}{2 x_{1}} & = x_{2} & x_{1} = 0 \Rightarrow x_{2} = 0 = x_{1} \\ \frac{x_{1}^{2} - 1 \pm \sqrt{1 - 2 x_{1}^{2} + x_{1}^{4} + 4 x_{1}^{2}}}{2 x_{1}} & = x_{2} \\ \frac{x_{1}^{2} - 1 \pm \sqrt{x_{1}^{4} + 2 x_{1}^{2} + 1}}{2 x_{1}} & = x_{2} \\ \frac{x_{1}^{2} - 1 \pm \sqrt{(x_{1}^{2} + 1)^{2}}}{2 x_{1}} & = x_{2} \\ \frac{x_{1}^{2} - 1 \pm | x_{1}^{2} + 1 |}{2 x_{1}} & = x_{2} \end{aligned}

Two cases since $| x_{1}^{2} + 1 | \geq 0$ :

( $+$ ):

x_{2} = \frac{x_{1}^{2} - 1 + x_{1}^{2} + 1}{2 x_{1}} = x_{1}

( $-$ ):

x_{2} = \frac{x_{1}^{2} - 1 - x_{1}^{2} - 1}{2 x_{1}} = \frac{- 1}{x_{1}}

So just choose the ( $+$ ) case! We are done.

(surjective): For scratch we are essentially trying to find $f^{- 1}$ . So try to swap the $x$ 's with $y$ 's and solve for $y$ :

\begin{aligned} f (y) & = x \\ \frac{y}{y^{2} - 1} & = x \\ y & = x (y^{2} - 1) \\ y & = x y^{2} - x \\ 0 & = x y^{2} - y - x \\ y & = \frac{1 \pm \sqrt{1 + 4 x^{2}}}{2 x} \end{aligned}

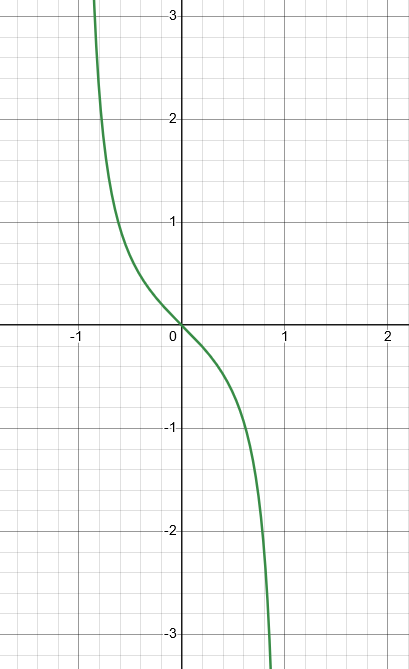
Pasted image 20241006004540.png

Which

\pm

do we use? We want all

x > 0

to have

y < 0

and all

x < 0

to be

y > 0

. The only choice we could do that is with

-

Thus let $y \in R$ . Choose $x \in (- 1, 1)$ where:

x = {\begin{cases} 0 & y = 0 \\ \frac{1 - \sqrt{1 + 4 y^{2}}}{2 y} & y \neq 0 \end{cases}

We claim that this is a good choice. Notice:

\begin{aligned} f (x) & = f (\frac{1 - \sqrt{1 + 4 y^{2}}}{2 y}) \\ = \frac{\frac{1 - \sqrt{1 + 4 y^{2}}}{2 y}}{{(\frac{1 - \sqrt{1 + 4 y^{2}}}{2 y})}^{2} - 1} \\ = \frac{1 - \sqrt{1 + 4 y^{2}}}{2 y} \cdot \frac{1}{\frac{1 - 2 \sqrt{1 + 4 y^{2}} + 1 + 4 y^{2}}{4 y^{2}} - 1} \\ = \frac{1 - \sqrt{1 + 4 y^{2}}}{2 y} \cdot \frac{1}{\frac{1 - 2 \sqrt{1 + 4 y^{2}} + 1 + 4 y^{2} - 4 y^{2}}{4 y^{2}}} \\ = \frac{1 - \sqrt{1 + 4 y^{2}}}{2 y} \cdot \frac{4 y^{2}}{2 (1 - \sqrt{1 + 4 y^{2}})} \\ = y \end{aligned}

Notice too that the non-trivial part of our cases for $y \neq 0$ never has the numerator equal 0, so then we are covered here.
☐