Cumulative Distribution Function (CDF)
CDF (Cumulative Distribution Function)
The cumulative distribution function (cdf)
For each
Using
Let
and for any two numbers
These come from the fact that
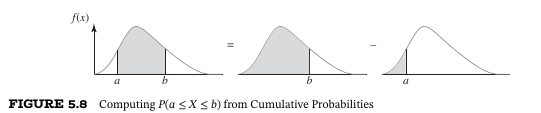
The cumulative distribution function (cdf)
For each
Let
and for any two numbers
These come from the fact that
