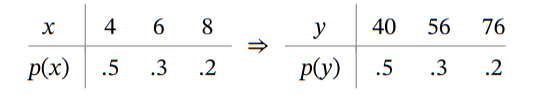Expected Value

expected value, mean value

Let $X$ be a discrete rv with a set of possible values $D$ and pmf $p (x)$ . The expected value or mean value of $X$ , denoted $E (X), μ_{X}, μ$ is:

E (X) = μ_{x} = μ = \sum_{x \in D} x \cdot p (x)

If you've used a weighted average, then this is what that is.

For example, given the following Probability Distribution, PMF:

Pasted image 20241003163847.png

Then the mean value of $X$ , $μ_{X}$ is:

μ_{X} = (0) (.002) + (1) (.001) + \dots + (10) (.01) = 7.15

Often $μ$ is NOT a value of $X$ , so we don't round it. It's just the center-of-mass for certain distribution of probabilities.

Expected Value of a Function

Often we are interested in the expected value of some function $h (X)$ rather than $X$ itself. We can compute this by just:

Getting our pmf in terms of $X$
Calculate each $y = h (x)$ for all $x \in X$
Say $p (y)$ for each $y$ corresponds to the old $x$ used to calculate $y$ .

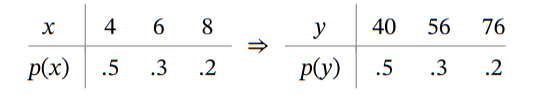
Pasted image 20241003164212.png

For instance for $h (X) = 20 + 3 X + .5 X^{2}$ (see the table above)

$X = 8$ implies $Y = h (8) = 20 + 3 (8) + .5 (8)^{2} = 76$
Thus $P (Y = 76) = P (X = 8) = .2$

Law of the Unconscious Statistician

If the rv $X$ has a set of possible values $D$ and pmf $p (x)$ , then the expected value of any function $h (X)$ denoted $E [h (X)]$ or $μ_{h (X)}$ is computed by:

E [h (X)] = \sum_{x \in D} [h (x) \cdot p (x)]

Linearity of Expectation

For any linear function $h (X) = a X + b$

E (a X + b) = a \cdot E (X) + b, μ_{a X + b} = a μ_{X} + b

Proof
Since $h$ is a linear function and $E$ is as well, then because they are linear maps gives the result above.
☐