Probability Distribution, PMF

probability distribution or probability mass function

For a discrete rv, the probability distribution is defined for every number $x$ by:

p (x) = P (X = x) = P ({s \in S | X (s) = x})

The support of pmf $p$ is the set of all $x$ values for which $p (x) > 0$ . We frequently display a pmf only for the values in its support, with the understanding that $p (x) = 0$ otherwise.

Example

Consider randomly selecting a student at a 4-year public university. Define bernoulli rv by $X = 1$ for a 1-st year, $X = 2$ for a second year, and so on up to 4th year. If there's an equal distribution of all years of student, then:

p (1) = p (2) = p (3) = p (4) = .25

Thus:

p (x) = {\begin{cases} .25 & x \in {1, 2, 3, 4} \\ 0 & x \notin {1, 2, 3, 4} \end{cases}

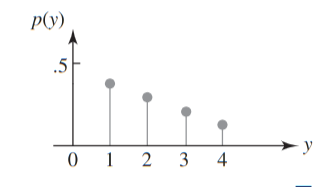
If our pmf is a table like:

$y$	1	2	3	4
$p (y)$	.4	.3	.2	.1
Then we can create a graph of our pmf:

Pasted image 20241003163505.png