Independence in Probability

Independence

Two events $A, B$ are independent if $P (A | B) = P (A)$ . Otherwise they are dependent.

Notice here:

P (B | A) = \frac{P (A \cap B)}{P (A)} = \frac{P (A | B) P (B)}{P (A)}

Here if $P (A) = P (A | B)$ when they're independent, then $P (B | A) = P (B)$ as a result. You also get equality for $P (A) = P (A | B^{'})$ and similar.

Disjoint vs. Independence

Being independent doesn't mean that $P (A | B) = 0$ , ie that $A \cap B = \emptyset$ . Instead, it just means that they are proportional in probabilities.

Mall Survey

Consider the following mall survey:
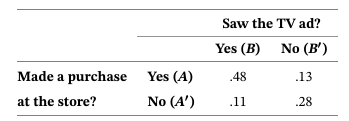
Pasted image 20240930231508.png
We got that $P (A) = .61$ while $P (A | B) = .81$ . Thus clearly $A, B$ are dependent.