The Law of Total Probability

Law of Total Probability

Let $A_{1}, . . ., A_{k}$ be a partition of the sample space $S$ . Then for any other event $B$ :

P (B) = P (A_{1}) \cdot P (A_{2} | A_{1}) + \dots + P (A_{k}) \cdot P (B | A_{k}) = \sum_{i = 1}^{k} P (A_{i}) P (B | A_{i})

Proof
Because the $A_{i}$ 's form a partition then if $B$ occurs it must be in conjunction with exactly one of the $A_{i}$ 's. This "partitioning" of $B$ is show in the figure below:

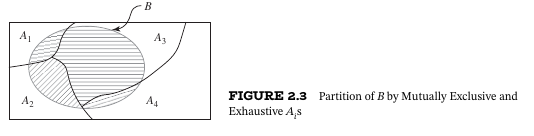
Pasted image 20240930225419.png

By the Multiplication Rule for Conjunct we have $P (A_{i} \cap B) = P (A_{i}) P (B | A_{i})$ so then:

P (B) = \sum_{i = 1}^{k} P (A_{i} \cap B) = \sum_{i = 1}^{k} P (A_{i}) P (B | A_{i})

☐

University Example

Say we have information on enrollment and six-year graduation rate for 4 campuses:
Pasted image 20240930225719.png
What is the overall six-year graduation rate for the entire system? Namely, what is the probability that a randomly selected student from this university system graduates within six-years?

Proof
Let's say $A_{i} = {student is from campus # i}$ for $i = 1, 2, 3, 4$ and $B = {the student graduated within six years}$ . For example $P (A_{1}) = .45$ , $P (B | A_{2}) = .58$ and so on.

Apply the Law of Total Probability:

P (B) = .45 \cdot .51 + .26 + .58 + \dots + .13 \cdot .64 = .5515

Notice that this is a weighted sum of the probabilities: schools with more enrollment get more of a say as to the number of six-year graduates.
☐