Definition of Conditional Probability

In general, calculating $P (A | B)$ , or the probability of $A$ given $B$ requires that the sample space is not $S$ anymore. Rather, it's now $B$ . An example will illustrate how this works:

Components Example

Say there are two assembly lines $A, A^{'}$ . $B$ indicates there was a defective component and $B^{'}$ as non-defective. We count the number of parts each line made, and whether they were defective or non-defective:
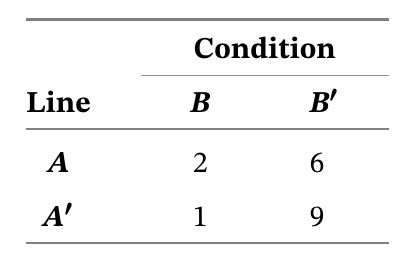
Pasted image 20240925091125.png
Here the probability a line $A$ component is selected is:

P (A) = \frac{N (A)}{N} = \frac{8}{18} = .444

However if the selected component was defective $B$ then we know that the component can only be from the $B$ column, so we consider that as our sample space. Thus:

P (A | B) = \frac{P (A \cap B)}{P (B)} = \frac{\frac{2}{18}}{\frac{3}{18}} = \frac{2}{3}

Thus we have the following definition:

P (A | B)

For any two events $A, B$ with $P (B) > 0$ , the conditional probability of $A$ given $B$ , denoted $P (A | B)$ , is defined as:

P (A | B) = \frac{P (A \cap B)}{P (B)}

Polytechnic University

A student at Cal Poly is randomly selected. Let $A$ denote the event the student is taking a statistics class, $B$ for a computer science class, and $C$ for a math class:
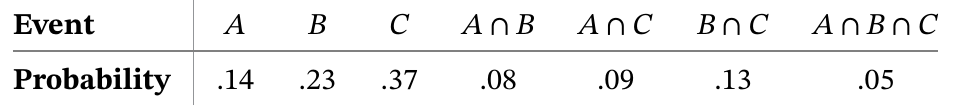
Pasted image 20240925091656.png
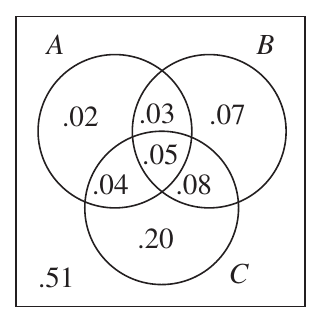
Pasted image 20240925091846.png
If the selected student is in $B$ , then the probability of $A$ is:

P (A | B) = \frac{P (A \cap B)}{P (B)} = \frac{.08}{.23} = .348

Given that the student is taking at least one of the subjects $A \cup B \cup C$ then:

P (A | A \cup B \cup C) = \frac{P (A \cap (A \cup B \cup C))}{P (A \cup B \cup C)} = \frac{P (A)}{P (A \cup B \cup C)} = \frac{.14}{.49} = .286

If the student is taking a math class, the change of taking one of the other two classes is:

P (A \cup B | C) = \frac{P ((A \cup B) \cap C)}{P (C)} = \frac{.04 + .05 + .08}{.37} = .459