Relative Frequency

If we have an experiment that can be repeatedly performed in an identical fashion, let $A$ be the event consisting of a fixed set of outcomes. If the experiment is performed $n$ times, sometimes $A$ will occur and on all the other times $A$ won't (so $A^{'}$ will). Let $N (A)$ denote the number of times $A$ occurs. Then the ratio $\frac{N (A)}{n}$ is called the relative frequency.

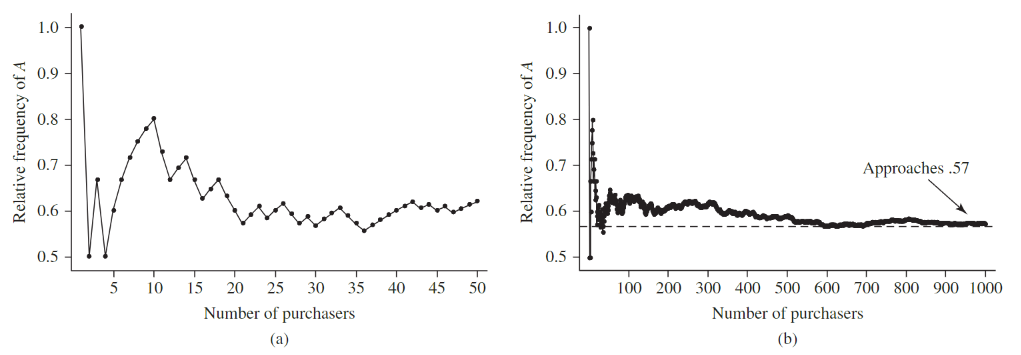
Pasted image 20240924091307.png

Normally this approaches a number as $n \to \infty$ . This limit it approaches is the long-run or limiting relative frequency. Probability objectively defines $P (A)$ as this probability:

P (A) = lim_{n \to \infty} \frac{N (A)}{n}

This is essentially the Law of Large Numbers.

Gambler's Fallacy

You cannot use the fact that you have a streak of some event $A$ to predict that $A^{'}$ will happen next. For example, if you flip 8 heads in a row, that doesn't tell you that tails is going to come next.

Why? Consider the next flip as the first flip! Now it doesn't matter that you flipped 8, 10, 100, or any large number of heads prior. Now you have started at square one, which shouldn't change your probability!

We say the limiting relative frequency is "objective" since it doesn't get dictated based on a small, possibly misrepresentative sample size. However, we can't realistically do an infinite number of experiments, so we usually have to base probabilities on accepted values. A fair coin has $P (H) = P (T) = 0.5$ ; nothing weird about that.

References

[[Matthew A. Carlton, Jay L. Devore - Probability with STEM Applications-Wiley (2020).pdf#page=44]]