Contingency Tables

Instead of Venn Diagrams, we can use contingency tables to show probabilities of combinations of events:

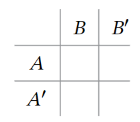
Pasted image 20240924102149.png

Here the upper-left entry is $P (A \cap B)$ , and similarly for the other cells. Since the cells all union to $S$ , their probabilities must add to 1. The sum of the $A$ row is $P (A)$ and the sum of the $B$ column is $P (B)$ .

Example

Using the residential properties example, we have $P (I), P (T), P (I \cap T)$ giving:

| | $T$ | $T^{'}$ | |
| ---- | --- | ---- | --- |
| $I$ | .5 | | .6 |
| $I^{'}$ | | | |
| | .8 | | |

Since $P (T^{'}) = 1 - P (T) = .2$ and $P (I^{'}) = 1 - P (I) = 0.4$ then we know the other totals. Doing similar deductions with the other properties of probabilty will give the total table:

| | $T$ | $T^{'}$ | |
| ---- | --- | ---- | --- |
| $I$ | .5 | .1 | .6 |
| $I^{'}$ | .3 | .1 | .4 |
| | .8 | .2 | 1.0 |

If you wanted to use the table to get say $P (I \cup T)$ then you would just use the addition rule:

P (I \cup T) = P (I) + P (T) - P (I \cap T) = .6 + .8 - .5 = .9

and so on.

References

[[Matthew A. Carlton, Jay L. Devore - Probability with STEM Applications-Wiley (2020).pdf#page=48]]