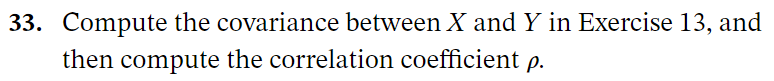Ch 7 - 13, 17, 33

7.13 (forgor k in c)

Question

Pasted image 20241025070203.png

Proof

\begin{aligned} \int_{20}^{30} \int_{20}^{30} f (x, y) d y d x & = k \int_{20}^{30} \int_{20}^{30} x^{2} + y^{2} d y d x \\ 1 & = k \cdot \frac{380000}{3} \\ \Rightarrow k & = \frac{3}{380000} \end{aligned}

\begin{aligned} P (X \land Y < 26) & = \int_{20}^{26} \int_{20}^{26} \frac{3}{380000} (x^{2} + y^{2}) d y d x \\ \approx .30 \end{aligned}

\begin{aligned} P (| X - Y | < 2) & = P (X - Y < 2 \land Y - X < 2) \\ = \frac{3}{380000} (\int_{20}^{22} \int_{20}^{x + 2} (x^{2} + y^{2}) d y d x + \int_{22}^{30} \int_{x - 2}^{x + 2} (x^{2} + y^{2}) d y d x) \\ \approx .3878 \end{aligned}

d. We want $p_{X} (x)$ which is:

\begin{aligned} p_{X} (x) & = \int_{all y} f (x, y) d y \\ = \int_{20}^{30} (x^{2} + y^{2}) d y \\ = 10 x^{2} + {[\frac{y^{3}}{3}]}_{20}^{30} \\ = 10 x^{2} + \frac{19000}{3} \end{aligned}

for $x \in [20, 30]$ .

e. Likely not. Notice by symmetry that:

p_{Y} (y) = 10 y^{2} + \frac{19000}{3}

p_{X} (x) \cdot p_{Y} (y) = (10 x^{2} + \frac{190000}{3}) \cdot (10 y^{2} + \frac{19000}{3}) = 100 x^{2} y^{2} + \dots

Which clearly isn't $f (x, y)$ . So they are not independent.
☐

Question

Pasted image 20241025073104.png

Proof

Here we have:

p_{X} (x) = e^{- x}, p_{Y} (y) = e^{- y} \Rightarrow f (x, y) = p_{X} p_{Y} = e^{- (x + y)}

a. We just found that $f (x, y) = e^{- (x + y)}$ .
b.

\begin{aligned} P (X, Y \leq 1) & = \int_{0}^{1} \int_{0}^{1} e^{- (x + y)} d y d x \\ \approx .3996 \end{aligned}

\begin{aligned} P (X + Y \leq 2) & = \int_{0}^{2} \int_{0}^{2 - x} e^{- (x + y)} d y d x \\ \approx .5940 \end{aligned}

d. We want to find $1 \leq X + Y \leq 2$ is a similar problem, except we remove the triangular region showed below:

Thus we have:

\begin{aligned} P (1 \leq X + Y \leq 2) & = P (X + Y \leq 2) - P (X + Y \leq 1) \\ \approx .5940 - \int_{0}^{1} \int_{0}^{2 - x} e^{- (x + y)} d y d x \\ \approx .5940 - .4968 \\ = .0972 \end{aligned}

☐

Question

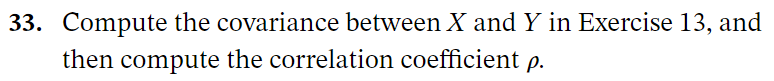
Pasted image 20241025074710.png
See 7.13 above.

Proof

p_{X} = 10 x^{2} +

\begin{aligned} μ_{X} & = \int_{all x} x \cdot p_{X} (x) d x \end{aligned}

☐