HW 7 (Practice) - Quantum Algorithms 2

1: QFT

Question

Consider the sequence of steps shown in Section 4 of the qiskit page on the Quantum
Fourier Transform: https://github.com/qiskit-community/qiskit-textbook/blob/main/content/ch-algorithms/quantum-fourier-transform.ipynb
a. Follow these steps explicitly for a 2-qubit system.
b. A two-qubit system can encode the numbers 0 to 3. For each of these find its Fourier
transform.
c. Is your result from the previous part consistent with the Bloch sphere animation at the
end of section 4 of the QFT qiskit textbook page? Explain. Since we only have three
qubits, which of the four spheres correspond to our three spheres (e.g. qubit 0 to 2 or
qubit 1 to 3, etc.).

For a 2-qubit system we can do the steps explicitly:

\begin{aligned} Q F T_{2} | x_{1} x_{2} ⟩ & = \frac{1}{\sqrt{2^{2}}} \sum_{y = 0}^{2^{2} - 1} ω_{4}^{x y} | y ⟩ \\ = \frac{1}{2} \sum_{y = 0}^{3} \exp (2 π i \frac{x y}{4}) | y ⟩ \\ = \frac{1}{2} (e^{2 π i \frac{x}{4} \cdot 0} | 00 ⟩ + e^{2 π i \frac{x}{4} \cdot 1} | 01 ⟩ + e^{2 π i \frac{x}{4} \cdot 2} | 10 ⟩ + e^{2 π i \frac{x}{4} \cdot 3} | 11 ⟩) \\ = \frac{1}{2} (\exp (2 π i x \cdot [\frac{0}{2^{1}} + \frac{0}{2^{2}}]) | 00 ⟩ \\ + \exp (2 π i x \cdot [\frac{0}{2^{1}} + \frac{1}{2^{2}}] | 01 ⟩) \\ + \exp (2 π i x \cdot [\frac{1}{2^{1}} + \frac{0}{2^{2}}] | 10 ⟩) \\ + \exp (2 π i x \cdot [\frac{1}{2^{1}} + \frac{1}{2^{2}}] | 11 ⟩)) \\ = \frac{1}{2} (\exp (2 π i x \frac{0}{2^{1}}) \exp (2 π i x \frac{0}{2^{2}}) | 00 ⟩) \\ + \frac{1}{2} (\exp (2 π i x \frac{0}{2^{1}}) \exp (2 π i x \frac{1}{2^{2}}) | 01 ⟩) \\ + \frac{1}{2} (\exp (2 π i x \frac{1}{2^{1}}) \exp (2 π i x \frac{0}{2^{2}}) | 10 ⟩) \\ + \frac{1}{2} (\exp (2 π i x \frac{1}{2^{1}}) \exp (2 π i x \frac{1}{2^{2}}) | 11 ⟩) \\ = \frac{1}{2} \exp (2 π i x \frac{0}{2^{1}}) | 0 ⟩ \otimes (\exp (2 π i x \frac{0}{2^{2}}) | 0 ⟩ + \exp (2 π i x \frac{1}{2^{2}}) | 1 ⟩) \\ + \frac{1}{2} \exp (2 π i x \frac{1}{2^{1}}) | 1 ⟩ \otimes (\exp (2 π i x \frac{0}{2^{2}}) | 0 ⟩ + \exp (2 π i x \frac{1}{2^{2}}) | 1 ⟩) \\ = \frac{1}{2} (| 0 ⟩ + \exp (2 π i x \frac{1}{2^{1}}) | 1 ⟩) \otimes (| 0 ⟩ + \exp (2 π i x \frac{1}{2^{2}}) | 1 ⟩) \end{aligned}

Encoding Numbers

Using our equation above, we can get our $Q F T_{2}$ for all the numbers:

Ket to Encode $\| x ⟩$	$Q F T_{2} \| x ⟩$
$\| 00 ⟩$	$Q F T_{2} \| x ⟩ = \frac{1}{2} (\| 0 ⟩ + \| 1 ⟩) \otimes (\| 0 ⟩ + \| 1 ⟩) = \frac{1}{2} (\| 00 ⟩ + \| 01 ⟩ + \| 10 ⟩ + \| 11 ⟩)$
$\| 01 ⟩$	$Q F T_{2} \| x ⟩ = \frac{1}{2} (\| 0 ⟩ - \| 1 ⟩) \otimes (\| 0 ⟩ + i \| 1 ⟩) = \frac{1}{2} (\| 00 ⟩ + i \| 01 ⟩ - \| 10 ⟩ - i \| 11 ⟩)$
$\| 10 ⟩$	$Q F T_{2} \| x ⟩ = \frac{1}{2} (\| 0 ⟩ + \| 1 ⟩) \otimes (\| 0 ⟩ - \| 1 ⟩) = \frac{1}{2} (\| 00 ⟩ - \| 01 ⟩ + \| 10 ⟩ - \| 11 ⟩)$
$\| 11 ⟩$	$Q F T_{2} \| x ⟩ = \frac{1}{2} (\| 0 ⟩ - \| 1 ⟩) \otimes (\| 0 ⟩ - i \| 1 ⟩) = \frac{1}{2} (\| 00 ⟩ - i \| 01 ⟩ - \| 10 ⟩ + i \| 11 ⟩)$
Notice that we can construct the unitary matrix in this case:

U_{Q F T} = \frac{1}{2} [\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & i & - 1 & - i \\ 1 & - 1 & 1 & - 1 \\ 1 & - i & - 1 & i \end{matrix}] \Leftrightarrow U_{I Q F T} = U_{Q F T}^{†} = \frac{1}{2} [\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & - i & - 1 & i \\ 1 & - 1 & 1 & - 1 \\ 1 & i & - 1 & - i \end{matrix}]

Intuition

Consider the following image:

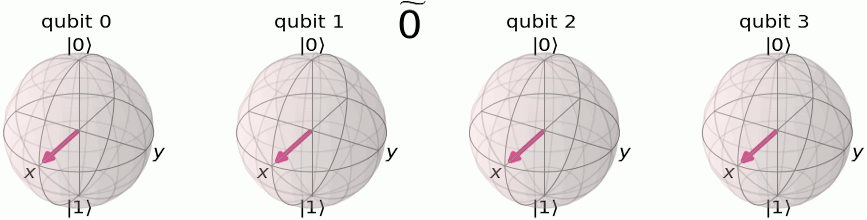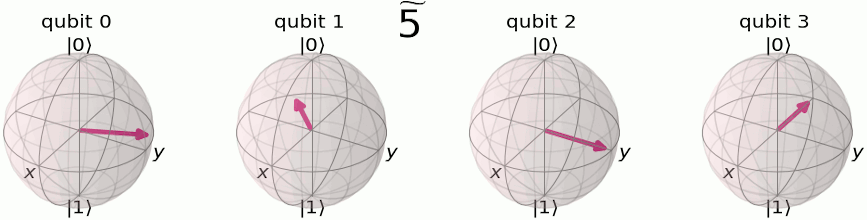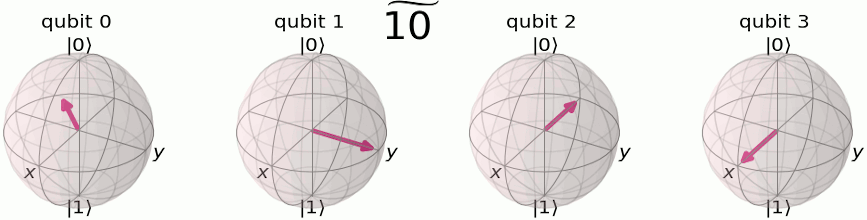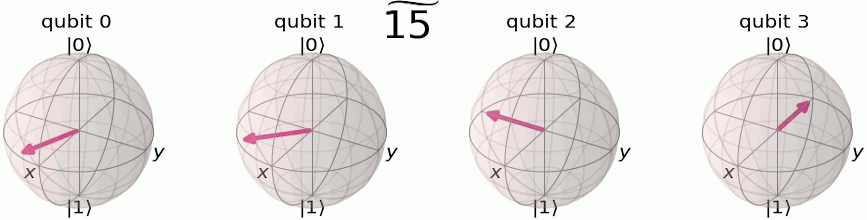
In this case since we have only two qubits, then qubit 3 in the gif above corresponds to the qubit 1 (the most significant qubit) in our 2-qubit system. Qubit 1 in our 2-qubit system corresponds to qubit 2 in the animation above.

This is because, if you look at the table prior, when the most significant qubit is changing between $| x ⟩$ states, it flips negative sign, which is exemplified in the animation. Similarly, the least significant bit changes the phase by $\frac{π}{2}$ radians, just like we see in the Qubit 2 animation above.

2: QPE

Question

Consider the sequence of steps shown in Section 1.2 of the qiskit page on the Quantum
Phase Estimation: https://github.com/qiskit-community/qiskit-textbook/blob/main/content/ch-algorithms/quantum-phase-estimation.ipynb
a. Follow these steps explicitly for a system with two counting qubits and one ancilla qubit.
b. Build this circuit in IBMQ. According to the resulting probability distribution, what is
θ?
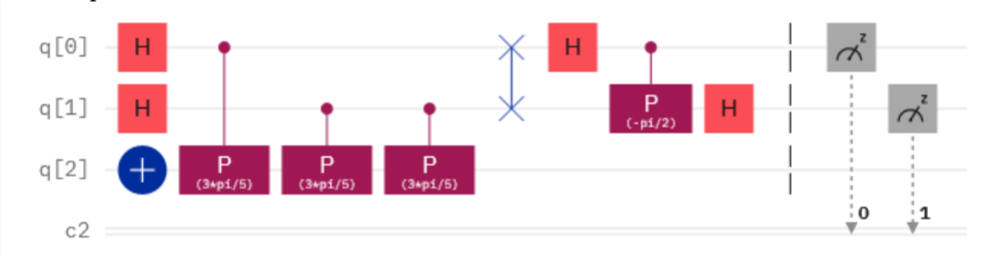
Pasted image 20240612091134.png
Explain.

A 2-qubit System

Consider running QPE for 2-qubits in our system (and still one ancilla qubit). Namely we want to find eigenvalues for the transformation $U$ that's arbitrary. Then:

| ψ_{0} ⟩ = {| 0 ⟩}^{\otimes 2} | ψ ⟩

Where it's presumed that $| ψ ⟩$ is an eigenvector of unitary $U$ . Applying the Hadamard Layer:

| ψ_{1} ⟩ = H^{\otimes 2} {| 0 ⟩}^{\otimes 2} | ψ ⟩ = \frac{1}{2} (| 0 ⟩ + | 1 ⟩) \otimes (| 0 ⟩ + | 1 ⟩) \otimes | ψ ⟩ = \frac{1}{2} (| 00 ⟩ + | 01 ⟩ + | 10 ⟩ + | 11 ⟩) | ψ ⟩

Applying the unitary operations:

\begin{aligned} | ψ_{2} ⟩ = U_{q_{1}}^{2} | ψ_{1} ⟩ & = \frac{1}{2} (| 00 ⟩ + | 01 ⟩ + U^{2} | 10 ⟩ + U^{2} | 11 ⟩) | ψ ⟩ \end{aligned}

| ψ_{3} ⟩ = U_{q_{0}}^{1} | ψ_{2} ⟩ = \frac{1}{2} (| 00 ⟩ + U | 01 ⟩ + U^{2} | 10 ⟩ + U^{3} | 11 ⟩) | ψ ⟩

All the $U$ 's only apply to the rightmost state by the way. So then:

| ψ_{3} ⟩ = \frac{1}{2} (| 00 ⟩ | ψ ⟩ + | 01 ⟩ U | ψ ⟩ + | 10 ⟩ U^{2} | ψ ⟩ + | 11 ⟩ U^{3} | 11 ⟩)

For each $U | ψ ⟩$ we are given that $U | ψ ⟩ = e^{2 π i θ} | ψ ⟩$ where $0 \leq θ \leq 1$ then:

| ψ_{3} ⟩ = \frac{1}{2} (| 00 ⟩ + e^{2 π i θ} | 01 ⟩ + e^{2 π i 2 θ} | 10 ⟩ + e^{2 π i 3 θ} | 11 ⟩) | ψ ⟩

Recall from earlier in our table that $θ$ can only be one of $| 00 ⟩, . . ., | 11 ⟩$ in resolution, so use the table for each gate going backwards. Namely we know:

U_{Q F T}^{†} = \frac{1}{2} [\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & - i & - 1 & i \\ 1 & - 1 & 1 & - 1 \\ 1 & i & - 1 & - i \end{matrix}]

Giving:

\begin{aligned} | ψ_{4} ⟩ & = \frac{1}{4} ((| 00 ⟩ + | 01 ⟩ + | 10 ⟩ + | 11 ⟩) \\ + e^{2 π i θ} (| 00 ⟩ - i | 01 ⟩ - | 10 ⟩ + i | 11 ⟩) \\ + e^{2 π i 2 θ} (| 00 ⟩ - | 01 ⟩ + | 10 ⟩ - | 11 ⟩) \\ + e^{2 π i 3 θ} (| 00 ⟩ + i | 01 ⟩ - | 10 ⟩ - i | 11 ⟩)) | ψ ⟩ \end{aligned}

\begin{aligned} | ψ_{4} ⟩ & = \frac{1}{4} \sum_{k = 0}^{3} \exp (2 π i k θ) | 00 ⟩ \\ + \frac{1}{4} \sum_{k = 0}^{3} \exp (2 π i k θ) \exp (2 π i \frac{3 π k}{2}) | 01 ⟩ \\ + \frac{1}{4} \sum_{k = 0}^{3} \exp (2 π i k θ) \exp (2 π i π k) | 10 ⟩ \\ + \frac{1}{4} \sum_{k = 0}^{3} \exp (2 π i k θ) \exp (2 π i \frac{k}{2}) | 11 ⟩ \\ = \frac{1}{4} \sum_{x = 0}^{3} \sum_{k = 0}^{3} \exp (- 2 π \frac{k}{4} (x - 2^{n} θ)) | x ⟩ \otimes | ψ ⟩ \end{aligned}

Thus we get a peak at ket $x = 2^{n} θ$ as then the exponent becomes a 1.

An Example System

Using the example system above, we get the following probability distribution:

Notice the spike in probability at $x = 1$ in this case. That implies that $2^{n} θ = 1$ so since $n = 2$ then $θ \approx \frac{1}{4}$ in this case.

3: Shor - period finding

Question

We want to carry out Shor's algorithm to factor 15.
a. Only one of the following options for $a$ meet the criteria for $a$ for use in Shor’s algorithm.
Which one is it? Circle the correct one. For all others, what is the reason they don’t
work?
i. $a = 5$
ii. $a = 12$
iii. $a = 13$
b. Using a = (the correct result from part a.), follow the cycle (until you get back to |1>)
shown in the first paragraph of section 2 on this page (and in class).
https://github.com/qiskit-community/qiskit-textbook/blob/main/content/ch-algorithms/shor.ipynb
c. Based on your result from the previous part, what is the period of $a^{x} \mod N$ ?

Which $a$ to use?

$a = 5$ will not meet the criteria. This is because $a$ itself is a factor for $N$ , so since we check if $a \mod N \equiv 0$ before we run Shor's, we'll never need to run it in this case.

$a = 12$ would not meet the criteria either. This is because $a$ also just contains a factor for $N$ . Namely, $gcd (a, N) = gcd (12, 15) = 3$ so then clearly $3$ would be a factor for $N$ and we wouldn't have to run Shor's Algorithm whatsoever.

$a = 13$ doesn't have the issues we've talked about above since $gcd (13, 15) = 1$ , so it's a valid candidate to use in the algorithm.

Using $a = 13$

Using this, we can execute Shor's Algorithm by hand. We'll use:

U | y ⟩ \equiv | 13 y \mod 15 ⟩

\begin{aligned} U^{1} | 1 ⟩ & = | 13 \mod 15 ⟩ \\ U^{2} | 1 ⟩ & \equiv | 4 \mod 15 ⟩ \\ U^{3} | 1 ⟩ & \equiv | 7 \mod 15 ⟩ \\ U^{4} | 1 ⟩ & \equiv | 1 \mod 15 ⟩ \end{aligned}

What does this show?

This shows that since the power $U^{4}$ returns our ket back to $\equiv | 1 \mod 15 ⟩$ then the power is our $r$ period, so $r = 4$ .

4: Shor - factoring

Question

Shor – factoring. Running a period finding algorithm, you found that with a choice of $a = 13$ , the period of $a^{x} \mod N$ is $r = 4$ .
a. Follow step 3 from lecture slide 33 to find two candidates for prime factors of $N$ .
b. If $N = 15$ , were any of our factors correct? If not, use step 4 from lecture slide 33 to find two new candidates for prime factors of 15. Now are any of your factors correct?

Finding $p, q$ Candidates

Given that $r = 4$ and $a = 13$ then since $r$ is even then we can use the candidates:

(a^{\frac{r}{2}} - 1) = (13^{\frac{4}{2}} - 1) = 168

(a^{\frac{r}{2}} + 1) = 2 + 168 = 170

Clearly neither of these are prime (they are both even), so we need to find the $gcd$ of $N$ and $a^{\frac{r}{2}} - 1$ with $N$ and $a^{\frac{r}{2}} + 1$ and $N$ :

gcd (N, 168) = 3

gcd (N, 170) = 5

These are the factors that we need for $N$ , so then $p = 3$ and $q = 5$ such that $N = p \cdot q$ .

Ket to Encode $\| x ⟩$	$Q F T_{2} \| x ⟩$
$\| 00 ⟩$	$Q F T_{2} \| x ⟩ = \frac{1}{2} (\| 0 ⟩ + \| 1 ⟩) \otimes (\| 0 ⟩ + \| 1 ⟩) = \frac{1}{2} (\| 00 ⟩ + \| 01 ⟩ + \| 10 ⟩ + \| 11 ⟩)$
$\| 01 ⟩$	$Q F T_{2} \| x ⟩ = \frac{1}{2} (\| 0 ⟩ - \| 1 ⟩) \otimes (\| 0 ⟩ + i \| 1 ⟩) = \frac{1}{2} (\| 00 ⟩ + i \| 01 ⟩ - \| 10 ⟩ - i \| 11 ⟩)$
$\| 10 ⟩$	$Q F T_{2} \| x ⟩ = \frac{1}{2} (\| 0 ⟩ + \| 1 ⟩) \otimes (\| 0 ⟩ - \| 1 ⟩) = \frac{1}{2} (\| 00 ⟩ - \| 01 ⟩ + \| 10 ⟩ - \| 11 ⟩)$
$\| 11 ⟩$	$Q F T_{2} \| x ⟩ = \frac{1}{2} (\| 0 ⟩ - \| 1 ⟩) \otimes (\| 0 ⟩ - i \| 1 ⟩) = \frac{1}{2} (\| 00 ⟩ - i \| 01 ⟩ - \| 10 ⟩ + i \| 11 ⟩)$
Notice that we can construct the unitary matrix in this case:

1: QFT

Encoding Numbers

Intuition

2: QPE

A 2-qubit System

An Example System

3: Shor - period finding

Which a to use?

Using a=13

What does this show?

4: Shor - factoring

Finding p,q Candidates

Which $a$ to use?

Using $a = 13$

Finding $p, q$ Candidates