HW 5 - Q. Computer Arch.

HW 5: 4.8, 4.10 (at least three different computers), explain in your words how the five DiVincenzo criteria are realized using neutral atoms

4.8

Question

How would you implement a CNOT Gate on a trapped ion qubit?

Proof
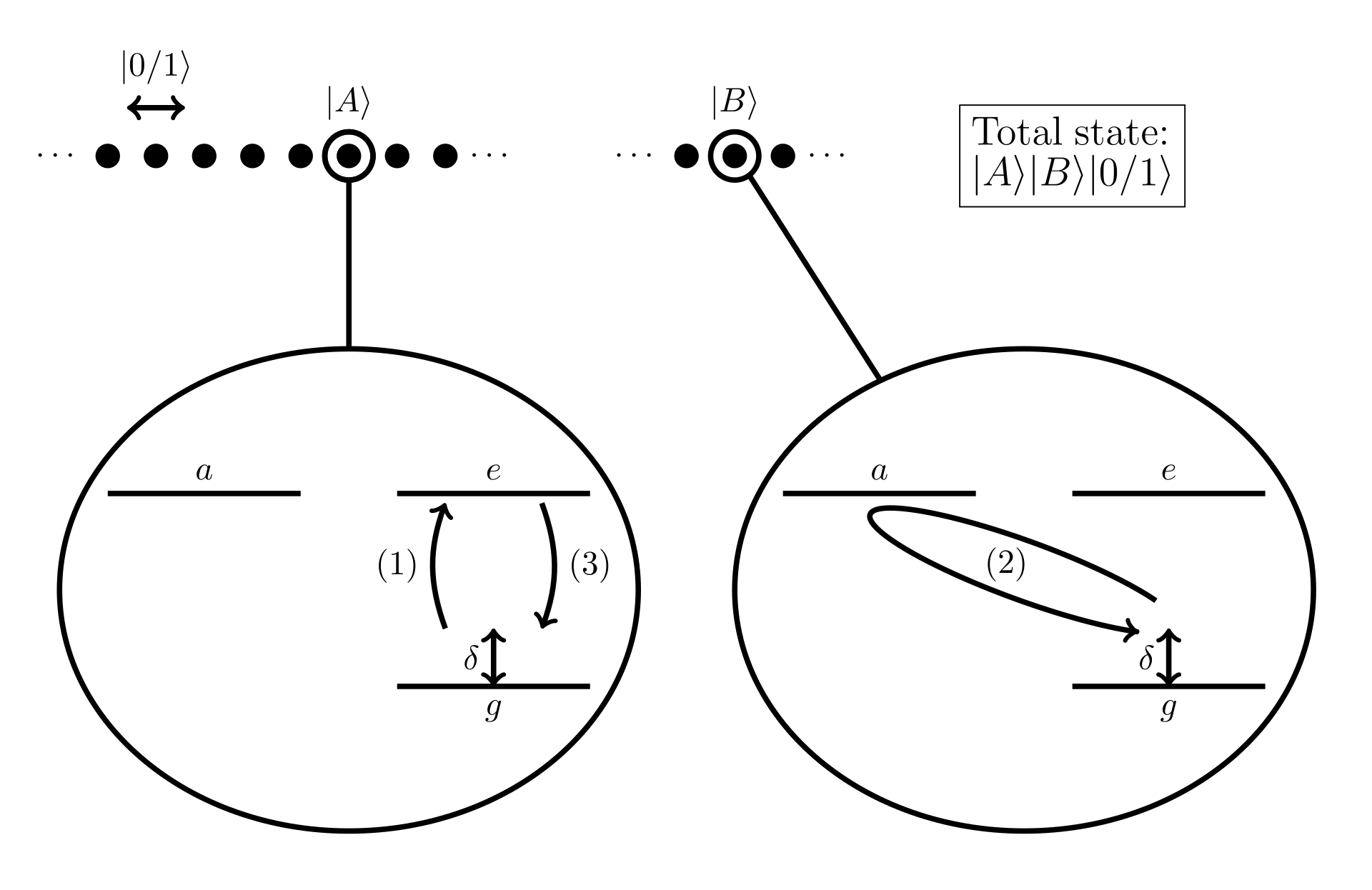
You would need to setup two $C a^{+}$ ions to act as our two qubits. The idea as proposed by Cirac-Zoller in their 1995 paper setting in stone the trapped-ion technology is as follows:

Pulse qubit $| A ⟩$ such that it goes from the ground state $g$ to the excited state $e$ using a $π$ pulse
Apply a $2 π$ pulse to $| B ⟩$ to some new state $a$ (the red sideband). This changes $| B ⟩$ 's phase if the state is in $g$ prior and $| A ⟩$ is excited as well.
Another red sideband $π$ pulse is applied to $| A ⟩$ to return it to the ground state $g$ .

☐

4.10

Question

Define quantum volume. Compute the quantum volume of commercially available quantum computers, based on publicly available information.

Proof
We define quantum volume similar to how a transistor count influences the performance metric of a classical computer. It is the largest width/depth (where equivalent) that's possible for a quantum circuit for that quantum computer. The numerical value is actually the area of this width/depth region, hence the idea of calling it a quantum "volume" specifically. For example, having a quantum volume of $2^{n}$ implies you can have the right output (likely) for an $n$ qubit circuit of up to $n$ layers of two-qubit gates.

The redefinition of quantum volume

While in 2018 Nikolaj Moll et al. coined and defined the term "quantum volume", IBM redefined it in 2019, and that definition (what's listed above) is the more standardized definition. However, the two are very related, where the Nikolaj Moll definition was similar to:

V_{Q} = min (N, d (N))^{2}

Where $V_{Q}$ is the quantum volume, $N$ is the number of qubits, and $d$ is the circuit depth. This is in constrast to the IBM definition using:

\log_{2} (V_{Q}) = max_{n \leq N} (min (n, d (n)))

Where here the difference is having $n$ be for circuit sizes considerably smaller than $N$ , and now $V_{Q}$ is some power of $2$ now (rather than being squared).

We can compute the quantum volume for some commercially available quantum computers:

Quantum Computer	Calculation/Sourcing	Quantum Volume $V_{Q}$
IBMQ	From this source, IBMQ hit a QV of 128, which is the figure on the right.	$2^{7}$
IonQ	Uses a slightly-different meaning algorithmic qubit but the idea is similar. But you have to take this with a grain of salt as it's a self-defined metric that's being converted back to a more standardized metric. This source claims the 35 AQ metric, which is similar to VQ by describing the power of 2. This source describes an older time that does the conversion, validating our process. The reason for the AQ metric is so that we can fix our number of qubits to something like 32 or 64, which usually is going to be more practical when hooking them up to classical computers. However, because if this the two metrics really aren't one to one. They're close approximations. Because they've gotten a huge depth, while the width is usually around 32, this determines that the lowest bound for QV must be to the power of 32 (as they can hit a considerably larger depth for quantum circuits).	$\sim 2^{35}$
Quantinuum	See this link. They also have a Github that shows where their calculations come from.	$2^{15}$

☐

DiVincenzo Criteria

The five DiVincenzo criteria are:

A scalable physical system with well characterized qubits
The ability to initialize the system to a known state
Ability to perform a universal set of quantum gates (some single and double-qubit gates)
Long Coherence Time
Ability to read out qubit state

Neutral Atom quantum computing accomplishes these because:

Neutral atom QC works at room temperature, and uses simple neutral atoms which are easy to put into quantum registers (groups of $R b$ or similar atoms) to help reduce the errors we get from the environment. The data for neutral atom qubits are held via the energy levels of electrons in these $R b$ atoms. They are also controllable because they can be better placed in bright/dark fringes of a controlled application of lasers, or even an electric field.
Applying specific lasers of the $F = 2 \to F^{'} = 1$ variety will cause it to fall back between the $F = 2$ or $| 1 ⟩$ state and $F = 1$ or $| 0 ⟩$ state. But since the laser keeps moving the $| 1 ⟩$ states back to an excited state, eventually all the qubits will fall back down to the $| 0 ⟩$ creating initialization.
Using varying lasers acts as our universal set of quantum gates. We can choose how focused we want our lasers to be, and thus how many qubits we want to act on. Specifically:
1. The intensity of the laser dictates the frequency $ω$ of the Rabi oscillations of qubits between $| 0 ⟩$ and $| 1 ⟩$ when acted on
2. The duration says how much $n π$ phase is applied to the qubit, creating some relative phase which is equivalent to rotation on the $y$ -axis of the bloch sphere.
3. The detuning gives more global phase by rotating around the $z$ -axis.
  Similarly, a two-qubit CNOT gate is done by:
  1. Putting the control qubit into a state $| r ⟩$ by applying a laser that moves it to that nearest energy level if the energy difference between $| 1 ⟩$ and $| r ⟩$ is small enough. In this way, the laser cannot move the control bit to $| r ⟩$ if it's currentlly $| 0 ⟩$ . This laser has $π$ phase
  2. Applying a $2 π$ pulse on the target qubit. If the control is in state $| r ⟩$ then the dipole interactions between it and the target means that it will not get the negative sign applied from having a $2 π$ pulse be applied.
  3. Applying the $π$ pulse to return from the $| r ⟩$ state applies a negative sign to all states where the control was previously in $| r ⟩$ .
Coherence times for neutral atom QC's can be influenced by the accidental absorpotion of photons from light patters that we use to hold the atoms in place. Using error correction by just having more atoms per qubit register helps extend these coherence times. Using actual error correction methods also help improve neutral atom QC-ing.
We read out the qubit states by sending an $F = 2 \to F^{'} = 3$ laser tuned to that frequency. A photodiode will collect some emitted light if the state was a $| 1 ⟩$ and if not detects a $| 0 ⟩$ .