Modules 1 & 2 - NMOS Review

Section 4.2: NMOS Equations

A summary of the needed NMOS equations is as follows:

NMOS Model Summary

For all regions:

K_{n} = K_{n}^{'} \cdot \frac{W}{L}, K_{n}^{'} = μ_{n} C_{o x}^{″} = μ_{n} \frac{ϵ_{o x}}{t_{o x}}, I_{G} = 0, I_{B} = 0

For the Cutoff Region, when $V_{G S} \leq V_{t n}$ :

V_{G S} \leq V_{t n} \Rightarrow I_{D} = 0

For the Triode Region, when $V_{G S} - V_{t n} \geq V_{D S} \geq 0$ :

I_{D} = K_{n} ((V_{G S} - V_{t n}) V_{D S} - \frac{1}{2} V_{D S}^{2})

For the Saturation Region, when $V_{D S} \geq V_{G S} - V_{t n} = V_{O V} \geq 0$ . If ideal, then $λ = 0$ :

I_{D} = \frac{K_{n}}{2} (V_{G S} - V_{t n})^{2} (1 + λ V_{D S})

The Threshold Voltage $V_{t n}$ is calculated via:

V_{t n} = V_{t o} + γ (\sqrt{v_{S B} + 2 ϕ_{F}} - \sqrt{2 ϕ_{F}})

Where $ϕ_{F}$ is the flat-band voltage of the ENMOS, seen in [[EE 306 MOSFETs Equation Sheet Fall 2023.pdf]], and $γ$ is the Body-effect parameter for the ENMOS.

There are some other parameters that we use to convert an NMOS to various formats, for instance, the transconductance $g_{m}$ is defined by:
SS

g_{m} = \frac{δ i_{D}}{δ v_{G S}} |_{Q_{p t}} = K_{n}^{'} \frac{W}{L} (V_{G S} - V_{t n}) = \frac{2 I_{D}}{V_{G S} - V_{t n}}

Further, the on-resistance is the resistance in the triode region near the origin, given by:

R_{o n} = {[\frac{δ i_{D}}{δ v_{D S}}]}^{- 1} |_{Q_{p t}} = \frac{1}{K_{n}^{'} \frac{W}{L} (V_{G S} - V_{t n} - V_{D S})} = \frac{1}{K_{n}^{'} \frac{W}{L} (V_{G S} - V_{t n})}

Sections 6.1-6.3: Inverter Characteristics - Digital Paradigm

6.1: Ideal Logic Gates

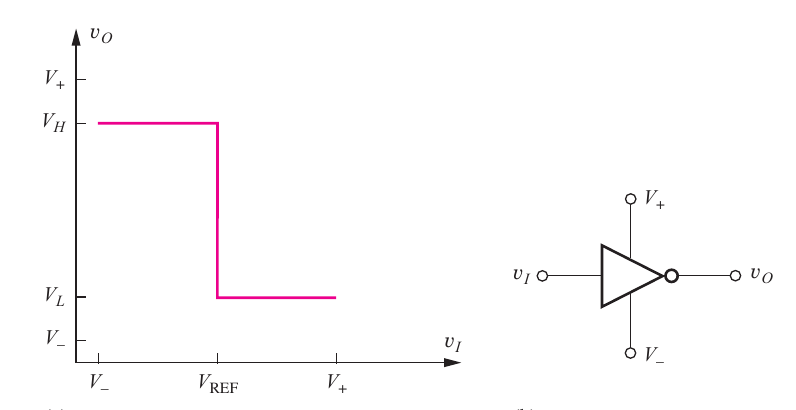
The logic symbol and voltage transfer characteristic (VTC) for an ideal inverter is given in the figure below:

Under $V_{R E F}$ is a logic low, ie: 0. So for this inverter, $V_{o}$ is a high logic level at the gate output
Over $V_{R E F}$ we have $V_{o}$ is low logic level.
$V_{+}, V_{-}$ are the power supply voltages to the gate provided. $V_{-} \approx 1.0 - 1.5 V$ now and $V_{+} \approx 1.8 - 3.3 V$ .

6.2: Logic Level Def's and Noise Margins

Really the inverter circuit is a voltage controlled switch:
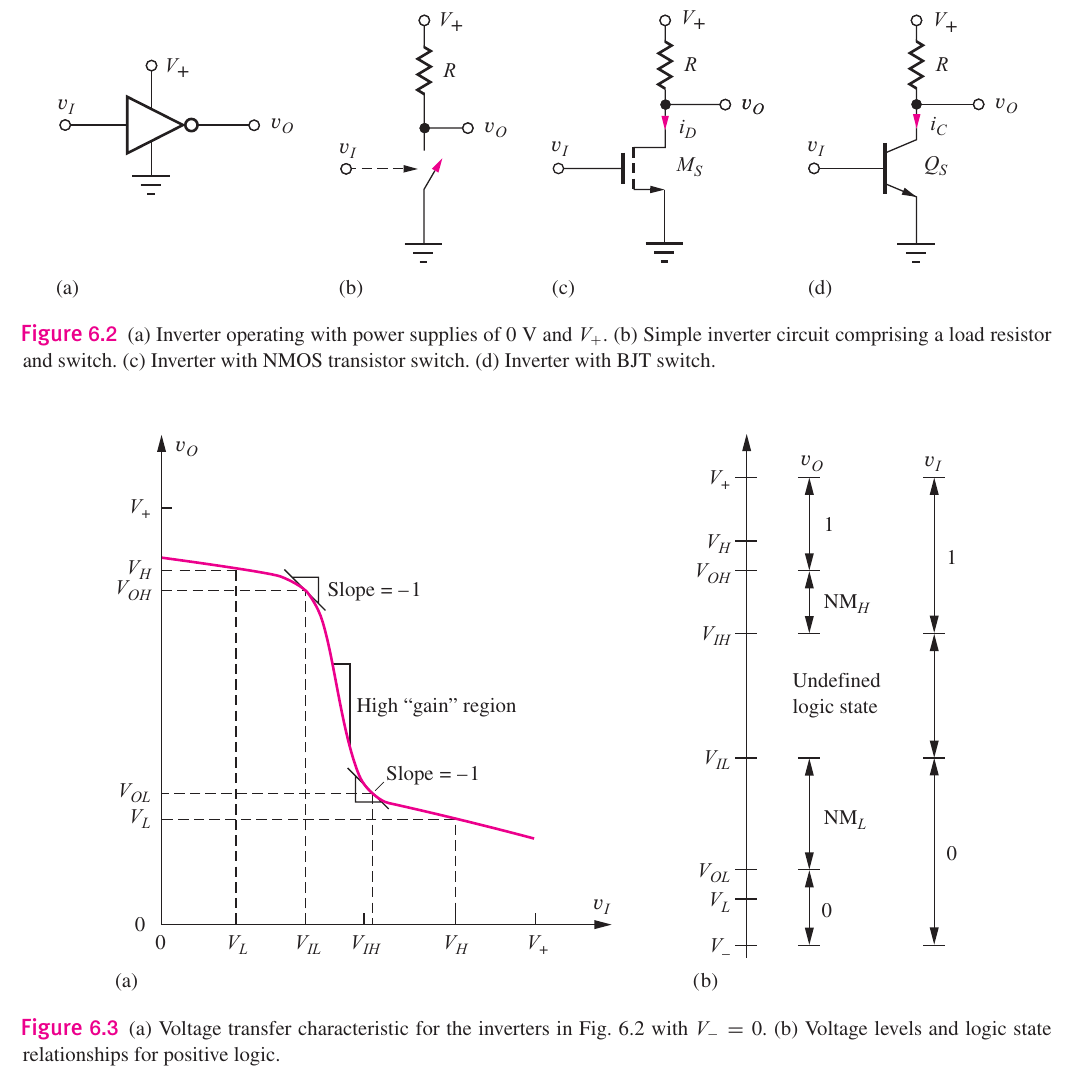
Pasted image 20240115194303.png

We either use a MOS transistor $M_{S}$ or a bipolar transistor $Q_{S}$ .
$V_{+}$ dictates the highest value $V_{H}$ when the transistor in question is off (no current flow)
$V_{L}$ often is not 0! We'll see this in later chapters.

The transfer curve in 6.3(a) shows how the transition from $V_{H}$ to $V_{L}$ (or vice versa) is really gradual.
When $V_{I} < V_{I L}$ which is the input low-logic-level, then we say that the input is logic low. Similarly, $V_{I} > V_{I H}$ implies an input high-logic-level. These are defined as when the slope is $- 1$ . The region in-between is an indeterminate logic level, which includes when the slope is $<< - 1$ . The points $V_{O H}, V_{O L}$ are the logic level voltages of $V_{H}$ at the points of $V_{I L}, V_{I H}$ respectively. We analyze this 'undefined' region later on. To summarize:

$V_{L}$ The nominal voltage corresponding to low-logic state at the output when $V_{I} = V_{H}$ . Generally, $V_{-} \leq V_{L}$ .
$V_{H}$ The nominal voltage corresponding to high-logic state at the output when $V_{I} = V_{L}$ . Generally $V_{+} \geq V_{H}$ .
$V_{I L}$ The max input voltage recognized as a low logic signal
$V_{I H}$ The min input voltage recognized as a high logic signal
$V_{O H}$ The output voltage corresponding to an input voltage of $V_{I L}$
$V_{O L}$ The output voltage corresponding to an input voltage of $V_{I H}$

For our purposes $V_{-} = 0 V$ , $V_{+} = 2.5, 3.3 V$ .

6.2.2 Noise Margins

Noise Margin in the high state $N M_{H}$ and same for the low state $N M_{L}$ are the margins allowed in the case that noise is introduced in the input to produce erroneous output
There may be resistance, capacitance, or inductance introduced into a PCB, thus we may have a lot of error over large amounts of gates. Using the definitions of the -1 slope points described above, we have the following:

N M_{L}, N M_{H}

$N M_{L} = V_{I L} - V_{O L}$ $N M_{H} = V_{O H} - V_{I H}$

Example

If a TTL gate has $V_{O H} = 3.6 V, V_{O L} = 0.4 V, V_{I H} = 2.0 V, V_{I L} = 0.8 V$ , then:

N M_{L} = 0.8 V - 0.4 V = 0.4 V, N M_{H} = 3.6 V - 2.0 V = 1.6 V

6.2.3 Logic Gate Design Goals

Goals for logic gates:

Minimize the width of the undefined input voltage range (ie: high noise margins)
Input shouldn't be affected by Output
Similar values of $V_{O L}, V_{O H}, . . .$ should be used among all gates
There should be allowed to have many different inputs to control one output, and many output to control an input of another gate
It should consume little power

6.3 Dynamic Response of Logic Gates

The clock speed of a processor is bottle necked by the propagation delay, rise time, ..., which are all things we now have control of.

6.3.1 Rise and Fall Time

rise time 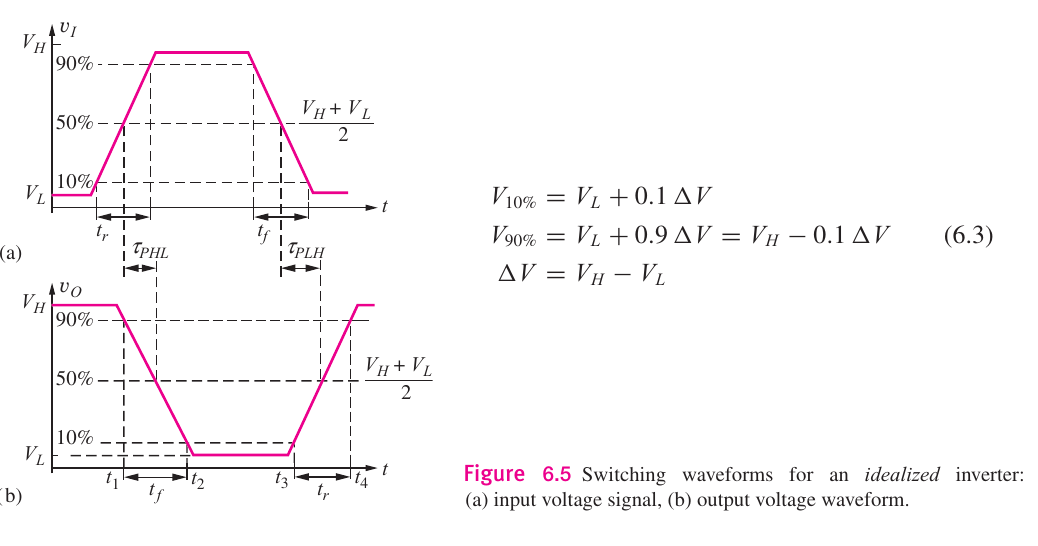$t_{r}$ is the time a signal takes from going from the 10% point to 90% point. The fall time $t_{f}$ is the same idea, but from going from 90% to 10% Pasted image 20240115202148.png
Here:

V_{10 %} = V_{L} + 0.1 Δ V

V_{90 %} = V_{L} + 0.9 Δ V = V_{H} - 0.1 Δ V

Δ V = V_{H} - V_{L}

6.3.2 Propagation Delay

Propagation Delay is the difference in time between the input and output signals reaching their 50% mark. The 50% point (in volts) is defined as:

V_{50 %} = \frac{V_{H} + V_{L}}{2}

The propagation delay on the high-to-low output transition is $τ_{P H L}$ and from low-to-high output transition is $τ_{P L H}$ . The average propagation delay is the average of the two:

τ_{P} = \frac{τ_{P L H} + τ_{P H L}}{2}

Example

Look at [[Pasted image 20240115202148.png]]. If $V_{L} = - 2.6 V$ and $V_{H} = - 0.6 V$ , and $t_{1} = 100 n s, t_{2} = 105 n s, t_{3} = 150 n s, t_{4} = 153 n s$ , what are $V_{10 %}, V_{90 %}, V_{50 %}, t_{r}, t_{f}$ ?

Proof
We know that:

\begin{aligned} Δ V & = V_{H} - V_{L} = 2.0 V \\ V_{10 %} & = V_{L} + 0.1 Δ V = - 2.4 V \\ V_{90 %} & = V_{H} - 0.1 Δ V = - 0.8 V \\ V_{50 %} & = \frac{V_{L} + V_{H}}{2} = - 1.6 V \\ t_{r} & = t_{4} - t_{3} = 3 n s \\ t_{f} & = t_{2} - t_{1} = 5 n s \end{aligned}

☐

6.3.3 Power-Delay Product

There's a power cost to switching a wire from 0 to 1 or vice versa, and for a whole gate there's an additive total cost. In low power regions, gate delay is dominated by inter gate wiring capacitance. But if we increase the power and device size, then we get limited by the speed of the electronic switching itself.

For our low-power purposes, we have it that the propagation delay decreases in direct proportion to the increase in power, so then the power-delay product (PDP) is defined as:

P D P = P τ_{P}

where $P$ is the average power dissipated by the logic gate.