HW 1 - NMOSReview + Inverter Characteristics

Chapter 4.2

4.9

Known (for NMOS):

V_{G S} = 0, 1, 2, 3

V_{D S} = 0.25

W = 5 μ m, L = 0.5 μ m, V_{t n} = 0.8 V, K_{n}^{'} = 200 \frac{μ A}{V^{2}}

We can create a table of each state for each value of $V_{G S}$ , which is dictated by:

V_{G S} \geq V_{t n}

When we are NOT in cutoff (in this case $V_{G S} \geq V_{t n}$ ), and furthermore consider when:

V_{D S} \circ V_{G S} - V_{t n} = V_{O V}

First, we can try to calculate $K_{n}$ via:

K_{n} = K_{n}^{'} \cdot \frac{W}{L} = 200 {\frac{μ A}{V}}^{2} \cdot \frac{5 μ m}{0.5 μ m} = 2 \frac{m A}{V^{2}}

We make the table using our value for $K_{n}$ :

Value of $V_{G S}$	Value of $V_{O V}$	Condition on $V_{G S}$	Condition on $V_{D S}$	Mode of Operation	Calculation of $I_{D S}$ (in A)
0	$- 0.8 V$	$V_{G S} < V_{t n}$	Don't Care	Cutoff	$I_{D S} = 0$
1	$0.2 V$	$V_{G S} \geq V_{t n}$	$0.25 = V_{D S} > V_{O V}$	Saturated	$I_{D S} = \frac{k_{n}}{2} (V_{G S} - V_{t n})^{2} = \frac{2 \frac{m A}{V^{2}}}{2} (1 V - 0.8 V)^{2} = 0.04 m A$
2	$1.2 V$	$V_{G S} \geq V_{t n}$	$0.25 = V_{D S} < V_{O V}$	Triode	$I_{D S} = k_{n} ((V_{G S} - V_{t n}) V_{D S} - \frac{1}{2} V_{D S}^{2})$ which is: $I_{D S} = 2 \frac{m A}{V^{2}} ((1.2 V) (0.25 V) - \frac{1}{2} (0.25 V)^{2})$ $I_{D S} = 0.5375 m A$
3	$2.2 V$	$V_{G S} \geq V_{t n}$	$0.25 = V_{D S} < V_{O V}$	Triode	Same as above, we get: $I_{D S} = 2 \frac{m A}{V^{2}} ((2.2 V) (0.25 V) - \frac{1}{2} (0.25 V)^{2})$ $I_{D S} = 1.0375 m A$

4.15

For this problem, the NMOS has a $W / L = 100$ and $V_{G S} = 5 V$ and $V_{t n} = 0.65 V$ . Table 4.6 gives that $K_{n}^{'} = 100 \frac{μ A}{V^{2}}$ .

a

The on-resistance is given by the equation:

R_{o n} = \frac{1}{K_{n}^{'} \frac{W}{L} (V_{G S} - V_{t n})} = \frac{1}{K_{n} (V_{G S} - V_{t n})}

Thus, we can plug in our values:

R_{o n} = \frac{1}{100 \frac{μ A}{V^{2}} \cdot \frac{100}{1} (5 V - 0.65 V)} \approx 23 Ω

b

If instead $V_{G S} = 2.5 V$ and $V_{t n} = 0.5 V$ , then we do the same thing:

R_{o n} = \frac{1}{100 \frac{μ A}{V^{2}} \cdot \frac{100}{1} (2.5 V - 0.5 V)} = 50 Ω

4.21

Given:

V_{G S} = 0, 1, 2, 3 V, V_{D S} = 4 V, W = 10 μ m, L = 1 μ m, V_{t n} = 1.5 V, K_{n}^{'} = 200 \frac{μ A}{V^{2}}

First, we can try to calculate $K_{n}$ per the question:

K_{n} = K_{n}^{'} \cdot \frac{W}{L} = 200 \frac{μ A}{V^{2}} \cdot \frac{10 μ m}{1 μ m} = 2 \frac{m A}{V^{2}}

We do something similar to HW 1 - NMOSReview#4.9:

Value of $V_{G S}$	Value of $V_{O V}$	Condition on $V_{G S}$	Condition on $V_{D S}$	Mode of Operation	Calculation of $I_{D S}$ (in A)
0	$- 1.5 V$	$V_{G S} < V_{t n}$	Don't Care	Cutoff	$I_{D S} = 0 A$
1	$- 0.5 V$	$V_{G S} < V_{t n}$	Don't Care	Cutoff	$I_{D S} = 0 A$
2	$0.5 V$	$V_{G S} \geq V_{t n}$	$4 = V_{D S} > V_{O V}$	Saturation	$I_{D S} = \frac{k_{n}}{2} (V_{G S} - V_{t n})^{2}$ Plugging in: $I_{D S} = \frac{2 \frac{m A}{V^{2}}}{2} (2 V - 1.5 V)^{2}$ $I_{D S} = 0.25 m A$
3	$1.5 V$	$V_{G S} \geq V_{t n}$	$4 = V_{D S} > V_{O V}$	Saturation	Same as above, we get: $I_{D S} = \frac{2 \frac{m A}{V^{2}}}{2} (3 V - 1.5 V)^{2} = 2.25 m A$

4.22

Given:

K_{n}^{'} = 200 \frac{μ A}{V^{2}}, W / L = 10, V_{t n} = 0.75 V

Notice then, for future calculations, that:

K_{n} = K_{n}^{'} \cdot W / L = 2 \frac{m A}{V^{2}}

a

We have:

V_{G S} = 2 V, V_{D S} = 2.5 V

We have then $V_{G S} \geq V_{t n}$ so we are not in cutoff. Furthermore:

V_{O V} = 1.25 V, 2.5 V = V_{D S} > V_{O V} = 1.25 V

So we are in the saturation region, so then:

I_{D} = \frac{K_{n}}{2} (V_{G S} - V_{t n})^{2} = \frac{2 \frac{m A}{V^{2}}}{2} (2 V - 0.75 V)^{2} = 1.5625 m A

b

We have:

V_{G S} = 2 V, V_{D S} = 0.2 V

We have then $V_{G S} \geq V_{t n}$ so not in cutoff.

V_{O V} = 1.25 V, V_{D S} < V_{O V}

So we are in the triode region:

I_{D} = K_{n} [(V_{G S} - V_{t n}) V_{D S} - \frac{1}{2} V_{D S}^{2}] = 2 \frac{m A}{V^{2}} [(1.25 V) (0.2 V) - \frac{1}{2} (0.2 V)^{2}] = 0.46 m A

c

We have:

V_{G S} = 0 V, V_{D S} = 4 V

We have that $V_{G S} < V_{t n}$ so we are in cutoff. Thus, $I_{D} = 0 A$ .

d

We replace our $K_{n}^{'}$ value with $300 \frac{μ A}{V^{2}}$ . Instead then:

K_{n} = K_{n}^{'} \cdot W / L = 3 \frac{m A}{V^{2}}

The findings are in the same regions as before, just with slightly different values:

Problem Part	Region of Operation	$I_{D}$
a	Saturation	$I_{D} = \frac{3 \frac{m A}{V^{2}}}{2} (2.0 V - 0.75 V)^{2}$ $I_{D} = 2.344 m A$
b	Triode	$I_{D} = 3 \frac{m A}{V^{2}} [(1.25 V) (0.2 V) - \frac{1}{2} (0.2 V)^{2}]$ $I_{D} = 0.69 m A$
c	Cuttoff	$0 A$

4.27

We are given that:

V_{G S} = 2 V, 3.3 V

Separately. In general:

V_{D S} = 3.3 V, W = 20 μ m, L = 1 μ m, V_{t n} = 0.7 V, K_{n}^{'} = 250 \frac{μ A}{V^{2}}

Thus:

K_{n} = K_{n}^{'} \cdot W / L = 5 \frac{m A}{V^{2}}

We can check for the necessary condition of being in the saturation region if we notice first that:

3.3 V = V_{D S} \geq V_{G S} - V_{t n} = 1.3 V, 2.7 V

Depending on whether we use the first, or second value for $V_{G S}$ . We also check:

V_{O V} = V_{G S} - V_{t n} = 1.3 V, 2.7 V \geq 0 V

Thus we aren't in cutoff, so therefore we are indeed in the saturation region. Thus, we can use the equation for transconductance:

g_{m} = K_{n} (V_{O V}) = 6.5, 13.5 \frac{m A}{V} = 6.5, 13.5 m S

For the corresponding values of $V_{G S}$ above.

4.30

Given:

K_{n} = \frac{500 μ A}{V^{2}}, V_{t n} = 1 V, V_{G S} = 4.0 V, V_{D S} = 5.0 V

For both parts, notice first that $V_{O V} = V_{G S} - V_{t n} = 3.0 V \geq 0$ so we aren't in cutoff. Further, $V_{D S} \geq V_{O V}$ so then we are always in saturation region (whether its ideal or not), so we use:

I_{D} = \frac{K_{n}}{2} (V_{G S} - V_{t n})^{2} (1 + λ V_{D S})

a

We first consider when $λ = 0.02 V^{- 1}$ . Then:

\begin{aligned} I_{D} & = \frac{0.5 \frac{m A}{V^{2}}}{2} (3.0 V)^{2} (1 + 0.02 V^{- 1} \cdot 5.0 V) \\ = 2.475 m A \end{aligned}

b

We now consider when $λ = 0 V^{- 1}$ . Then:

\begin{aligned} I_{D} & = \frac{K_{n}}{2} (V_{O V})^{2} \\ = \frac{0.5 \frac{m A}{V^{2}}}{2} (3.0 V)^{2} \\ = 2.25 m A \end{aligned}

4.32

We'll find the drain current in the NMOS transistor configuration given by:

First, we get some values for free from Table 4.6:

W / L = 10 \Rightarrow K_{n} = K_{n}^{'} \cdot W / L = 100 \frac{μ A}{V^{2}} \cdot 10 = 1 \frac{m A}{V^{2}}

V_{t n} = 0.75 V

Some work before getting into the problem, notice that, we'll just assume that we are in the saturation mode, so then:

I_{D} = I_{R}, \frac{12 V - V_{D}}{100 k Ω} = I_{D} = \frac{K_{n}}{2} (V_{G S} - V_{t n})^{2} (1 + λ V_{D S})

a

We first consider $λ = 0$ , so then:

\begin{align} \frac{12V - V_{GS}}{100k\Omega} &= \frac{1 \frac{mA}{V^2}}{2}(V_{GS} - 0.75V) {#2} \\ \Rightarrow 12V - V_{GS} &= 50(V_{GS}^2 - 1.5V_{GS} + 0.5625V) \\ 12V - 28.125V &= 50V_{GS}^2 - 74V_{GS} \\ 0 &= 50V_{GS}^2 - 74V_{GS} + 16.125V\\ \Rightarrow V_{GS} = \frac{74 \pm \sqrt{74^2 - 4\cdot50\cdot16.125}}{2\cdot 50} &= 1.214V, 0.266V\\ \end{align}

We know that $V_{G S} \geq V_{t n} = 0.75 V$ so then $V_{G S} = 1.214 V$ . Therefore:

\begin{aligned} V_{G S} & = 1.214 V \\ \Rightarrow I_{D} & = 0.108 m A \end{aligned}

b

We do the same thing except when $λ = 0.025 V^{- 1}$ . Then we get (replacing $V_{D S} = V_{G S}$ ):

\begin{aligned} \frac{12 V - V_{G S}}{100 k Ω} & = \frac{1 \frac{m A}{V^{2}}}{2} (V_{G S} - 0.75)^{2} (1 + λ V_{G S}) \\ 12 V - V_{G S} & = 0.5 \frac{m A}{V^{2}} (V_{G S}^{2} - 1.5 V_{G S} + 0.5625) (1 + 0.025 V_{G S}) \end{aligned}

We can intersect the LHS function with the RHS function to see where they intersect on a graphing calculator. This gives:

V_{G S} = 1.15 V \Rightarrow I_{D} = 108.5 μ A

c

If we repeat HW 1 - NMOSReview#a then we get that $W / L = 25$ , so then we have:

K_{n} = K_{n} \cdot W / L = 100 \frac{μ A}{V^{2}} \cdot 25 = 2.5 \frac{m A}{V^{2}}

So then:

\begin{aligned} \frac{12 V - V_{G S}}{100 k Ω} & = \frac{2.5 \frac{m A}{V^{2}}}{2} (V_{G S} - 0.75 V)^{2} \\ \Rightarrow 12 V - V_{G S} & = 250 (V_{G S}^{2} - 1.5 V_{G S} + 0.5625 V) \\ \Rightarrow 0 & = 250 V_{G S}^{2} - 374 V_{G S} + 128.625 V \\ \Rightarrow V_{G S} & = 0.960 V, 0.536 V \end{aligned}

Again we know $V_{G S} \geq V_{t n}$ so then $V_{G S} = 0.960 V$ , thus:

I_{D} = 110 μ A

4.34

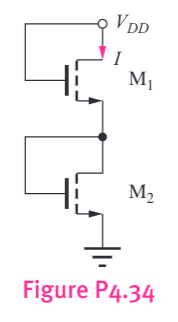
Consider the following:
Pasted image 20240115181224.png
Notice that $V_{G S 1} = V_{D S 1}$ and likewise $V_{G S 2} = V_{D S 2}$ . Likewise, we know $V_{D} D = 10 V = V_{D S 1} + V_{D S 2}$ . The strategy here is to assume that both are in Saturation, and check that both $V_{G S} \geq V_{t n}$ and that $V_{D S} > V_{G S} - V_{t n}$ . In those cases we use:

I_{D} = \frac{K_{n}}{2} (V_{G S} - V_{t n})^{2} (1 + λ V_{D S})

for various $λ$ .

a

Assume that $M_{1}, M_{2}$ are both in saturation. Then we get $I_{D}$ as described above, where $I_{D 1} = I_{D 2} = I$ . Notice that for both $M_{1}, M_{2}$ we are given that both identically have the same $W / L$ and thus the same $K_{n}$ value (since they use the same $K_{n}^{'}$ value). Thus:

\frac{K_{n}}{2} (V_{G S 1} - V_{t n})^{2} (1 + λ V_{G S 1}) = \frac{K_{n}}{2} (V_{G S 2} - V_{t n})^{2} (1 + λ V_{G S 2})

Simplify both sides and substitute $λ = 0$ .

\begin{aligned} (V_{G S 1} - V_{t n})^{2} & = (V_{G S 2} - V_{t n})^{2} \\ V_{G S 1} - V_{t n} & = V_{G S 2} - V_{t n} \\ V_{G S 1} & = V_{G S 2} \end{aligned}

Thus since $V_{G S 1} + V_{G S 2} = 10 V$ then $V_{G S 1} = 5 V = V_{G S 2} > V_{t n} = 0.75 V$ , which affirms our assumptions of Saturation. Further, $V_{D S 1} = 5 V > V_{G S 1} - V_{t n} = 4.25 V$ to further validate our assumption. Therefore, we can use the fact that $K_{n} = W / L \cdot K_{n}^{'} = 10 \cdot 100 \frac{μ A}{V^{2}} = 1 \frac{m A}{V^{2}}$ to get:

I_{D} = \frac{1 \frac{m A}{V^{2}}}{2} (5 V - 0.75 V)^{2} = 9.03 m A

b

We repeat except that $W / L = 20$ so then $K_{n} = 20 \cdot 100 \frac{μ A}{V^{2}} = 2 \frac{m A}{V^{2}}$ , to get:

I_{D} = \frac{2 \frac{m A}{V^{2}}}{2} (5 V - 0.75 V)^{2} = 18.06 m A

c

We repeat, except using $λ = 0.04 V^{- 1}$ :

\begin{aligned} (V_{G S 1} - V_{t n})^{2} (1 + λ V_{G S 1}) & = (V_{G S 2} - V_{t n})^{2} (1 + λ V_{G S 2}) \\ (V_{G S 1}^{2} - 2 V_{t n} V_{G S 1} + V_{t n}^{2}) (1 + λ V_{G S 1}) & = (V_{G S 1}^{2} - 2 V_{t n} V_{G S 1} + V_{t n}^{2}) (1 + λ V_{G S 1}) \\ . . . \end{aligned}

One needn't check that since the polynomial on the LHS and RHS are the same, we can easily determine that $V_{G S 1} = V_{G S 2} = 5 V$ yet again, and as before we verify that $V_{G S} > V_{t n}$ and $V_{D S} > V_{G S} - V_{t n}$ for both $M_{1}, M_{2}$ . Except this time we have:

I_{D} = \frac{1 \frac{m A}{V^{2}}}{2} (5 V - 0.75 V)^{2} (1 + 0.04 V^{- 1} \cdot 5 V) = 10.84 m A

4.43

We are given:

\begin{aligned} V_{G S} & = 0, 1, 2, 3 V \\ V_{D S} & = 4 V \\ W = 10 μ m \\ L = 1 μ m \\ V_{S B} = 1.5 V \end{aligned}

And given the Table's data:

\begin{aligned} V_{t o} & = 0.75 V \\ γ & = 0.75 \sqrt{V} \\ 2 ϕ_{F} & = 0.6 V \\ K_{n}^{'} & = 100 μ A / V^{2} \end{aligned}

We know for an NMOS transistor that:

V_{t n} = V_{t o} + γ (\sqrt{v_{S B} + 2 ϕ_{F}} - \sqrt{2 ϕ_{F}})

So then we can solve for $V_{t n}$ :

V_{t n} = 0.75 V + 0.75 \sqrt{V} (\sqrt{1.5 V + 0.6 V} - \sqrt{0.6 V}) = 1.256 V

We know:

K_{n} = K_{n}^{'} \cdot W / L = 10 \cdot \frac{100 μ A}{V^{2}} = 1 \frac{m A}{V^{2}}

We do something similar to HW 1 - NMOSReview#4.9:

Value of $V_{G S}$	Value of $V_{O V}$	Condition on $V_{G S}$	Condition on $V_{D S}$	Mode of Operation	Calculation of $I_{D S}$ (in A)
0	$- 1.256 V$	$V_{G S} < V_{t n}$	Don't Care	Cutoff	$I_{D S} = 0 A$
1	$- 0.256 V$	$V_{G S} < V_{t n}$	Don't Care	Cutoff	$I_{D S} = 0 A$
2	$0.744 V$	$V_{G S} \geq V_{t n}$	$4 = V_{D S} > V_{O V}$	Saturation	$I_{D S} = \frac{1 \frac{m A}{V^{2}}}{2} (2 V - 1.256 V)^{2} = 0.278 m A$
3	$1.744 V$	$V_{G S} \geq V_{t n}$	$4 = V_{D S} > V_{O V}$	Saturation	$I_{D S} = \frac{1 \frac{m A}{V^{2}}}{2} (3 V - 1.744 V)^{2} = 1.521 m A$

Chapter 6.1-3

6.3

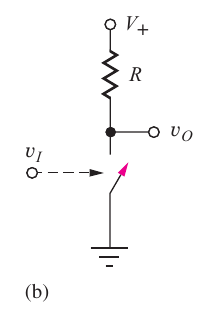
We are given the following inverter circuit:

Pasted image 20240115203823.png

We know then that since it's ideal, when $V_{I} > V_{I H}$ then $V_{O} = V_{L}$ and vice versa (since it's an inverter circuit), so then either $V_{O} = 0$ or $V_{O} = V_{+}$ .

a

$R = 100 k Ω$ and $V_{+} = 2.5 V$ . When $V_{o} = V_{H} = 2.5 V$ then we get no current flow through the resistor, $I_{R} = 0$ . But when we have $V_{o} = 0.0 V$ then we get a voltage difference over the resistor of:

I_{R, V_{o} = 0} = \frac{2.5 V - 0 V}{100 k Ω} = 25 μ A

Thus, the power draw for each of when we have:

P_{V_{H}} = I_{R, V_{H}}^{2} R = 0^{2} \cdot 100 k Ω = 0 W

and:

P_{V_{L}} = I_{R, V_{L}}^{2} R = (25 μ A)^{2} \cdot 100 k Ω = 62.5 μ W

b

We have the same reasoning as before, so we get:

I_{R, V_{o} = 0} = \frac{3.3 V - 0 V}{100 k Ω} = 33 μ A

Thus:

P_{V_{H}} = I^{2} R = 0^{2} \cdot 100 k Ω = 0 W

P_{V_{L}} = (33 μ A)^{2} \cdot 100 k Ω = 108.9 μ W

6.4

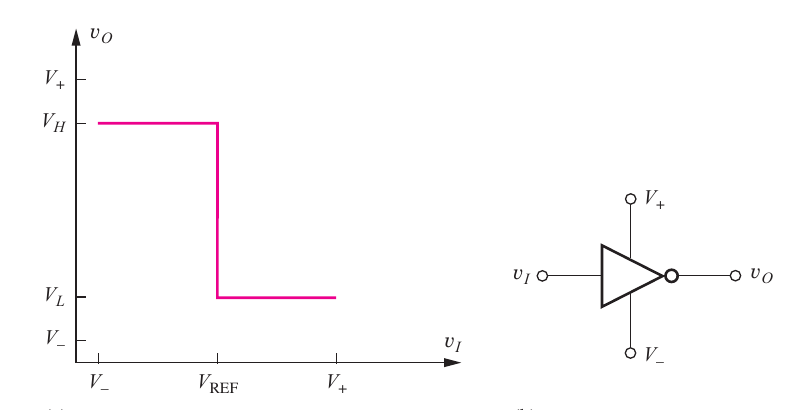
We'll plot the voltage transfer characteristic for an ideal inverter with $V_{+} = 2.5 V$ and $V_{-} = 0 V$ and $V_{R E F} = 0.8 V$ . We assume $V_{H} = V_{+}$ and $V_{L} = V_{-}$ :

6.5

a

We do the same thing as HW 1 - NMOSReview#6.4, but with two cascaded inverters:

b

The overall logic expression is $Z = f (A) = A$ , so it's just the identity.

6.6

We may want to see our other graph from Figure 6.1 to help us draw this:
Pasted image 20240115194029.png
Thus, our voltage gain graph $A_{v} = \frac{\partial v_{o}}{\partial v_{i}}$ looks like the following:

In essence, in the ideal case $A_v$ is just the *dirac delta function* $\delta(v_i) = v_o$.

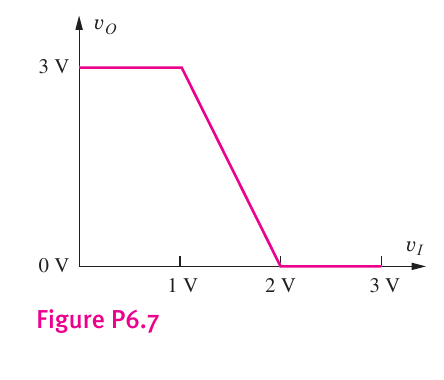
6.7

Given the graph:
Pasted image 20240115224118.png
What are $V_{H}, V_{L}, V_{I H}, V_{I L}$ ? We summarize:

V_{H} = 3 V, V_{L} = 0 V, V_{I H} = 2 V, V_{I L} = 1 V

The $A_{v}$ of this given function looks like the following:

6.8

If we had two cascaded inverters following Figure: Pasted image 20240115224118.png

Then we'd get the following complete graph...

Essentially here, if the function given is some $f(v)$, then we are considering the cascade as a composition of two of said function $f\circ f$.

6.9

Given that $V_{H} = 5 V, V_{L} = 0 V, V_{R E F} = 2.0 V$ , then using Figure 6.1:

V_{I H} = V_{I L} = 2.0 V

V_{O H} = 5 V, V_{O L} = 0 V

Therefore:

N M_{L} = V_{I L} - V_{I H} = 0.0 V

N M_{H} = V_{O H} - V_{O L} = 5 V

6.10

We should ideally have $V_{R E F}$ in the midpoint between $V_{H}$ and $V_{L}$ , so then:

V_{R E F} = \frac{V_{H} + V_{L}}{2} = 1.65 V

Note that this works for our noise margins to, specifically the one for our outputs gets maximized:

N M_{H} = V_{O H} - V_{O L} = 3.3 V - 0 V = 3.3 V

N M_{L} = V_{I L} - V_{I H} = 0.0 V

6.20

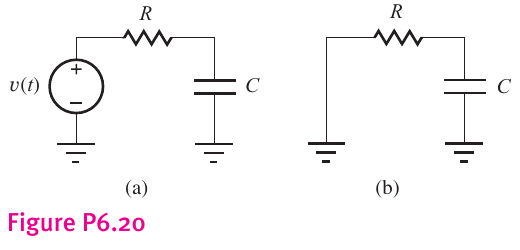
We consider the following circuits:
Pasted image 20240115231842.png

a

We can just use the equation for a series RLC circuit:

V_{C} (t) = V_{S} [1 - \exp (\frac{- t}{R C})] + V_{c} (0) \exp (\frac{- t}{R C})

Here we have $V_{S} = 1 V$ and $V_{c} (0) = 0 V$ (assuming the capacitor is uncharged), giving us:

V_{C} (t) = 1 - \exp (\frac{- t}{R C})

Note that we'll use $R C = τ$ as it is the time constant here. To get the rise time $t_{r}$ we need to find $V_{10 %}$ and $V_{90 %}$ . Here we know that $V_{H} = 1 V$ and $V_{L} = 0 V$ :

V_{10 %} = 0.1 V, V_{90 %} = 0.9 V

Thus we need to find the times $V_{c} (t_{10 %})$ and $V_{c} (t_{90 %})$ . We start with the former:

V_{c} (t_{10 %}) = 1 - \exp (\frac{- t_{10 %}}{τ}) = 0.1

\Rightarrow - \ln (0.9) τ = t_{10 %}

In a similar way we derive that:

\Rightarrow - \ln (0.1) τ = t_{90 %}

Thus, in this case to get the rise-time $t_{r}$ :

t_{r} = t_{90 %} - t_{10 %} = τ (\ln (0.9) - \ln (0.1)) \approx 2.197 τ

Thus, $t_{r} \propto τ$ .

b

In a similar way to HW 1 - NMOSReview + Inverter Characteristics#a, we know that now:

V_{C} (t) = \exp (\frac{- t}{τ})

So then, using the same $V_{H}, V_{L}$ :

V_{c} (t_{10 %}) = \exp (\frac{- t_{10 %}}{τ}) = 0.1 V

\Rightarrow - τ \ln (0.1) = t_{10 %}

And likewise:

\Rightarrow - τ \ln (0.9) = t_{90 %}

Thus, to get the fall-time $t_{f}$ :

t_{f} = t_{10 %} - t_{90 %} = τ (\ln (0.9) - \ln (0.1)) \approx 2.197 τ

Thus, $t_{f} \propto τ$ .

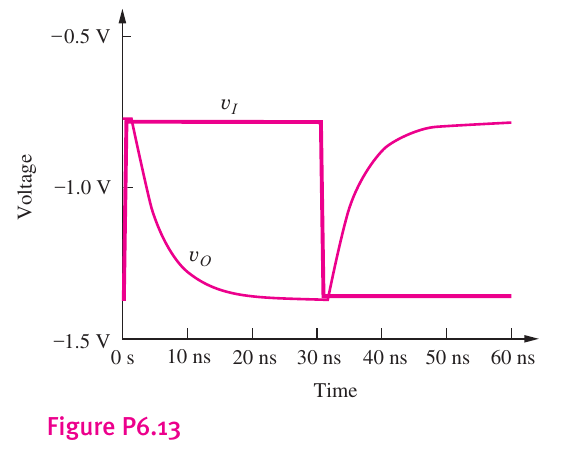
6.22

Consider the graph:

Pasted image 20240115234133.png

(a) Here $V_{H} \approx - 0.8 V$ and $V_{L} \approx - 1.4 V$ .

(b) The rise and fall times for $V_{I}$ are nearly instantaneous. For $V_{o}$ , the fall and rise times are pretty similar in length. Focusing on the fall times, it appears that $t_{10 %}$ for voltage $V_{10 %} \approx - 1.34 V$ is at $t_{10 %} \approx 20 n s$ . Furthermore, for $t_{90 %} \approx 2.5 n s$ , so then:

t_{f} \approx 20 n s - 2.5 n s = 17.5 n s

(c) We note that $τ_{P H L} \approx τ_{P L H}$ as they're pretty symmetric. Note that $V_{50 %} \approx - 1.1 V$ so then $t_{50 %} \approx 8 n s$ . Thus:

τ_{P L H} = t_{50 %} - t_{90 %} = 8 n s - 2.5 n s = 6.5 n s

Likewise $τ_{P H L} \approx 6.5 n s$ .

(d) Since $τ_{P H L} \approx τ_{P L H}$ then $τ = τ_{P H L} = 6.5 n s$ .