Lab 3 is due today. Program 2 is due in 2 weeks. Lab 4 will be all about what we talk about today, which is Matrix transformation of 3D scenes for rasterization.

The final project for this class should reflect your interests. You'll want to find some objs (more than one) to make a cool scene that really reflects your interests.

As an aside, for Program 2 the key task is to setup and move geometry (via our matrix transformations).

Matrices

Recall from Lecture 4 - Finishing Rasterizer, Moving to OpenGL. We need to have the GPU use the parallelism and matrix multiplication specialization of it to compute our graphics.

Think of it like the following diagram:

To minimize data transfer, we send the GPU a geometric data array, like so:

Really, we give the GPU all the data beforehand, then make GL calls to tell the GPU "rasterize this object, light up this object, ...". We just only have to then send one command during runtime.

But what if the tree is suddenly far away? Scaled up? Etc.?

That's where geometric transforms come into play.

Geometric Transforms and the Model Matrix

We use a $4\times 4$ matrix to model our matrix, called the model matrix. Say, for our example, we send our treeVAO object, which is on the GPU. We send model matrices for each instance of our treeVAO:

Here each $M_1,...,M_4$ is a matrix that the GPU handles computing to transform each object separately.

For example, consider:

// simple_vert.glsl
uniform mat4 M; //model
uniform mat4 P; //perspective (ignore for now)
uniform mat4 V; //view (ignore for now)


void main()
{
	gl_Position = P * V * M * vec4(vertPos, 1.0);
	// we'll focus on M * vec4(vertPos, 1.0); for L4 first!!!
	fragCol = vec3(0.1, 0.3, 0.1);
}

Then, the code that actually draws the function is in render/draw call (glDrawArrays more specifically).

So for animation, there's a variable like i that you send to the GPU for updating, and then have it update that and have the transform matrices depend on that variable (for example, rotation, you can send some $\theta$ variable that gets updated).

So in main you need to:

• Create our VAO
• Send the data to the GPU. On there, each object individually gets a compute module to get worked on.

But okay how do we do the Geometric Transform? What are these mysterious matrices?

The Matrices

Recall:

Vectors are 3-components, with no position. They are a change in position.

We can add vectors $v,w$ via:

We use tip-to-tail to draw vectors being added to each other:

We can also scale our vector by a magnitude $\alpha$:

We also have the dot product:

where:

So like:

But let's think about this geometrically.

$v\cdot w$ is the length of the projection of $v$ onto $w$.

Matrices

We have matrices in $2\times 2$ and $3\times 3$ matrices like:

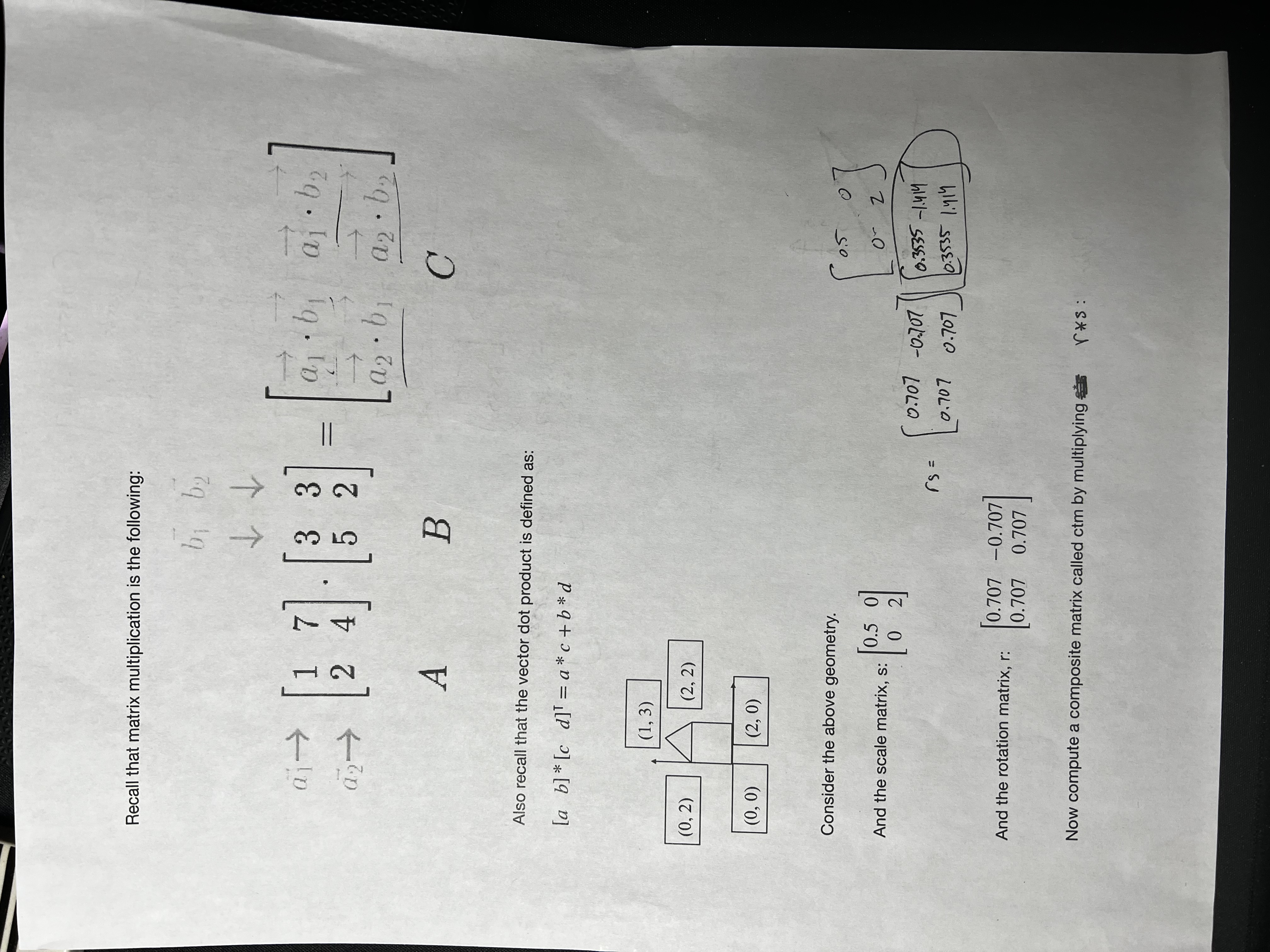
Let's review matrix multiplication:

Notice that the input vector just gets scaled by 2, so if we want to encode scaling by a factor, we can make the scale matrix:

scaled by a factor $\alpha$. If we want rotation matrix by 45 degrees it's:

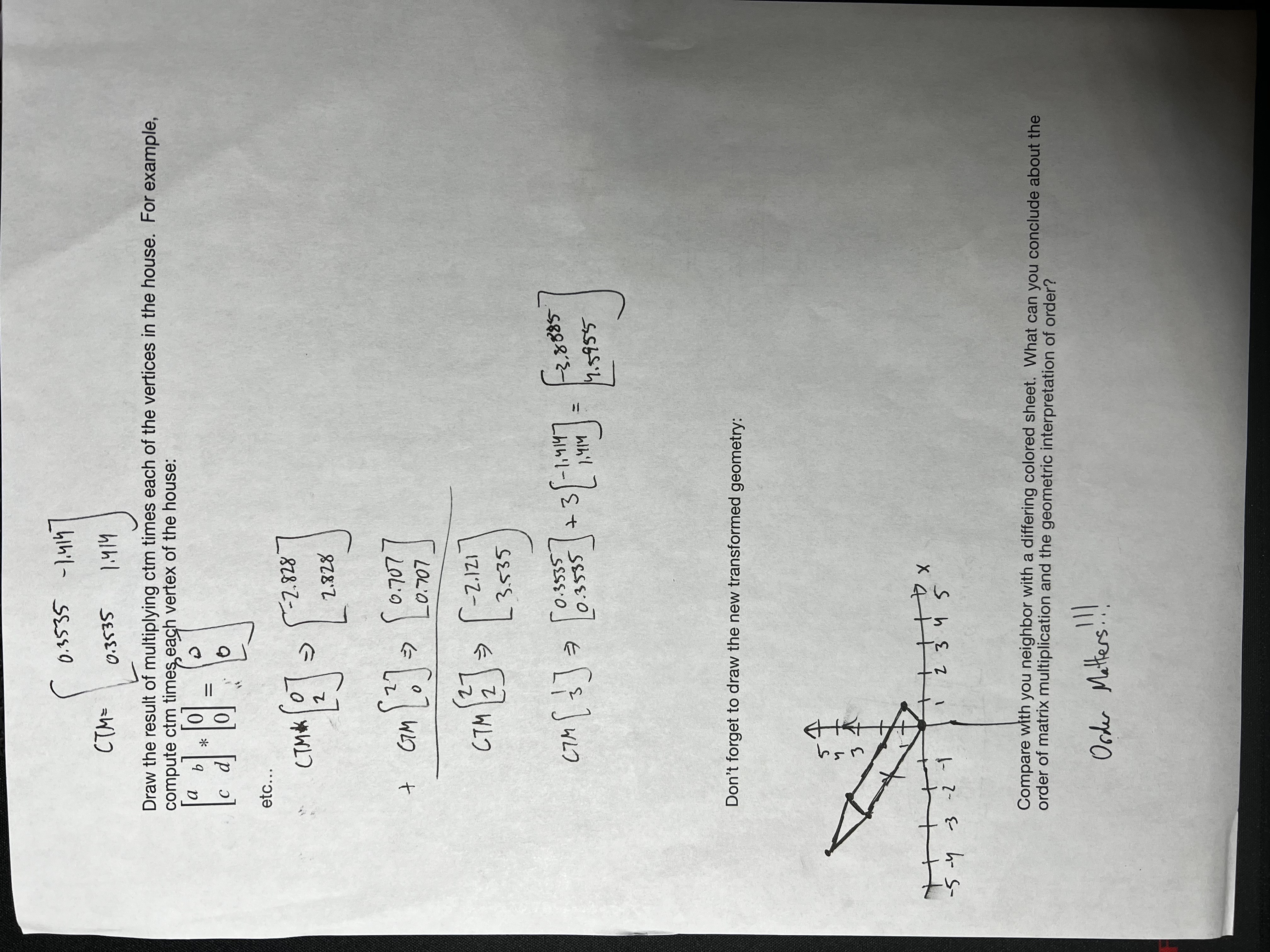
The worksheet we did reviews a lot of this information: