Lecture 2 - The Big Picture (literally)

Reminders

Strike info will be sent out later down the pipeline

Real-Time Interactive Comp. Graphics Applications

Goal: My program draws something to the screen, and my program can possibly animate it. The user should be able to interact with the program.

This is a big goal! So we'll break it up. Our first goal is rasterization, making a rasterizer (project 1). This will be about drawing a single static picture. The code outline is:

Starting the Rasterizer

We are given an obj file, full of indexed face sets (see Lecture 1 - Syllabus and Starting Graphics). Recall that:

Points are described by vertices (ie: singular vertex)
We describe our data in our world space
We need a way to map our 3D coordinates to our 2D pixel space.
An easy way is to set all $z$ 's to 0.
This is a projection, and there's multiple types, like orthographic.

Don't worry about the details. Just note that our projection will be setting all $z$ 's to 0 (which is orthographic projection). This implies we are just looking down the $z$ axis.

World space is a place where our artists can build their worlds. Notice though that:

Vertices are anything, they are any $R^{3}$ .
Pixel coordinates must instead be in $0 \leq x_p \leq \text{width} - 1 (and similar for $y$ ).
- We need some bounds. Starting at $(0, 0)$ in the bottom-left, we need the maximum, top right corner so we don't write outside the pixel space.

So the big thing you have to do here is: make a transformation from our 3D space of $R^{3}$ to 2D limited-width version of $R^{2, \leq window}$ .

Note

Since our pixel space will have to, eventually, cut off items in our world space. In a similar way, us as programmers can cut off items themselves in the world space.

Conflicts in Seeing the Items

Notice that, if we see two items, we need to consider the order that we render objects. We won't solve this yet, but keep it in mind.

Rasterizer Overview (How to Build)

Thus, for our P1 rasterizer, we need to:

Read in our obj file to get vertices in world coordinates.
Convert the world to pixel coordinates (will set boundaries in the world based on window size)
Do a depth test to only write the $△$ 's in the front
We only have the vertices colored in! So color the bounding triangle (ie: rasterize the triangle) and decide which pixels to color in.

The big question is 4. How do we decide the pixel to color in?

Line Rasterization

One of the early algorithms was line rasterization. Notice that there's 3 lines per triangle. You've seen the equation as $y = m x + b$ . But this is a crappy line equation. A better one to use is the parametric line equation:

\begin{aligned} x & = (1 - t) x_{0} + t x_{1} \\ y & = (1 - t) y_{0} + t y_{1} \end{aligned}

Note that usually $t \in [0, 1]$ , which is good. We can subdivide our line into some number of chunks $n$ , and then consider $t \in {0, 1 / n, 2 / n, . . ., n / n}$ .

t > 1

t < 0

, you get the points that are on the direction of the line, but just outside of the edge in question (either past or front of the line).

Consider the barycentric coordinates:

v^{'} = α v_{a} + β v_{b} + γ v_{c}

where $γ = 1 - α - β$ .

This seems confusing, but look at this worksheet:

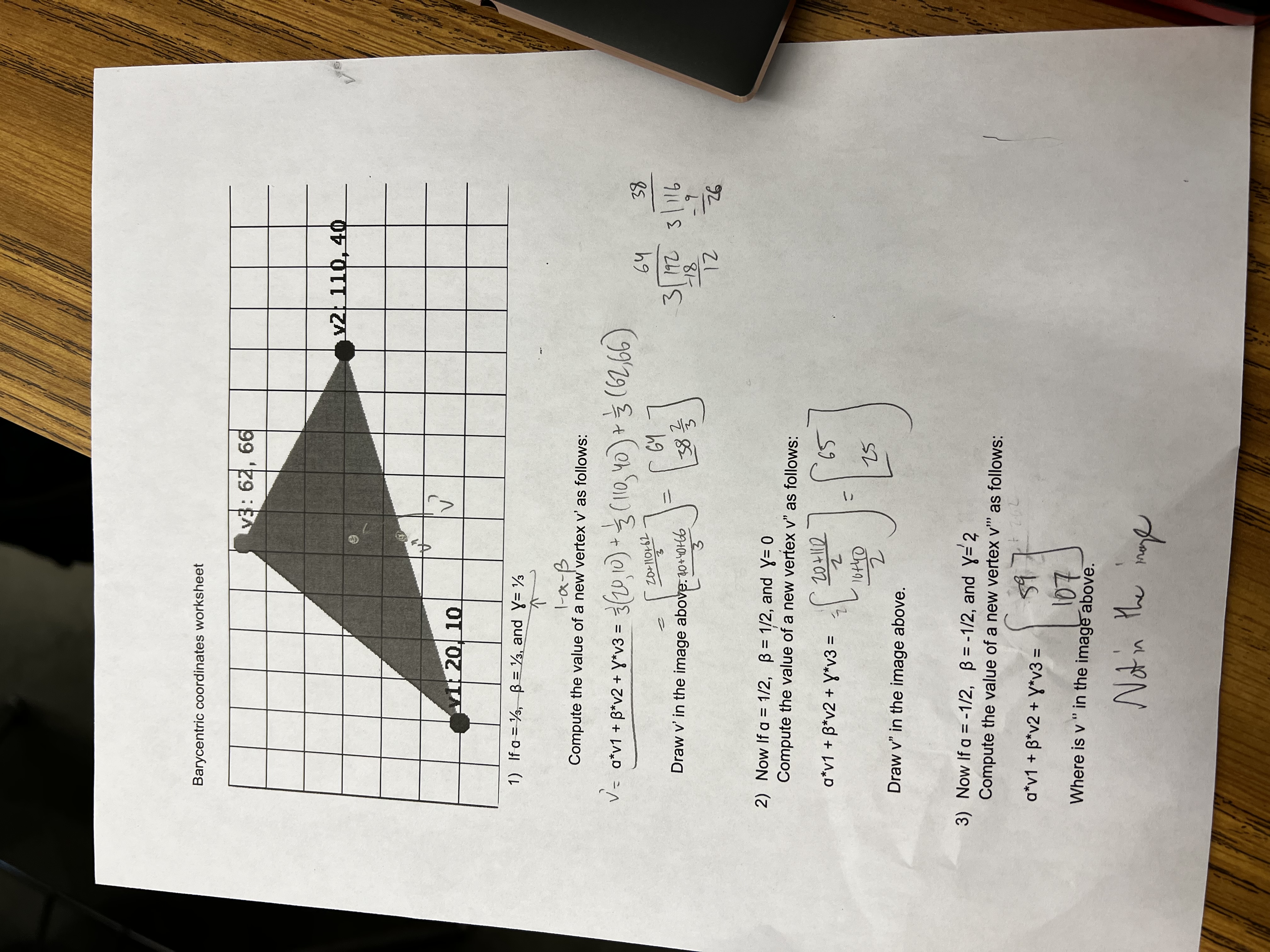
The idea here is that if $α, β, γ = \frac{1}{3}$ , we get the center of the triangle. If two are $1 / 2$ and the other is $0$ , we get the midpoint of one of the edges. Here, if $α, β, γ$ are randomly generated, we can get a bunch of random points in the triangle.

But what if we go backwards? Given a pixel coordinate, can we solve for $α, β, γ$ ? If so, we can tell if we're in the triangle (none are negative).

Therefore: the idea here is:

Get the bounding box for the triangle (from Lab 1)
Determine the values of $α, β, γ$ for each pixel. If $0 \leq α \leq 1$ , (and similar for $β, γ$ ), then draw the point (the appropriate color)

We can use these as well to color the pixels based on the colors of our triangle's vertices, and then use $α v_{a} + β v_{b} + γ v_{c}$ for each color to color the new pixel with that color.

More on Barycentric Coordinate Intuition

The way to think about this is that the areas of the triangles opposite to the point in question are the proporitions of $α, β, γ$ :

So then:

\begin{aligned} α & = \frac{Area of sub △}{Area of whole △} = \frac{A a}{A} \\ β & = \frac{A b}{A} \\ γ & = \frac{A c}{A} \end{aligned}

Recall from Linear Analysis I that, if you have two edges ${\vec{e}}_{1}, {\vec{e}}_{2}$ that make up two of the $△$ 's edges, we can get the area of one triangle bounded by the two points (and the origin) via:

\frac{1}{2} | | {\vec{e}}_{1} \times {\vec{e}}_{2} | |

Know that the determinant is needed here:

| \begin{matrix} e_{1 x} & e_{2 x} \\ e_{1 y} & e_{2 y} \end{matrix} | = e_{1 x} e_{2 y} - e_{2 x} e_{1 y}

So the process is:

A_{b} = | \begin{matrix} x - v_{c x} & v_{a x} - v_{c x} \\ y - v_{c y} & v_{a y} - v_{c y x} & v_{a x} - v_{c x} \end{matrix} |

So:

Computer $A$ , the area of this big $△$
For every pixel in bounding box of this triangle, compute $α = Area of sub triangle / A$ . Repeat for the other coefficients ( $β, γ$ ). For the latter, we can just do $γ = 1 - α - β$ .
If all coefficients are between 0 and 1, use the coefficients to draw our weight colors.